Which hemisphere is the observer?

[guv]

TL;DR Summary: Astro Olympiad Problem determining the latitude of an observer from a picture taken.

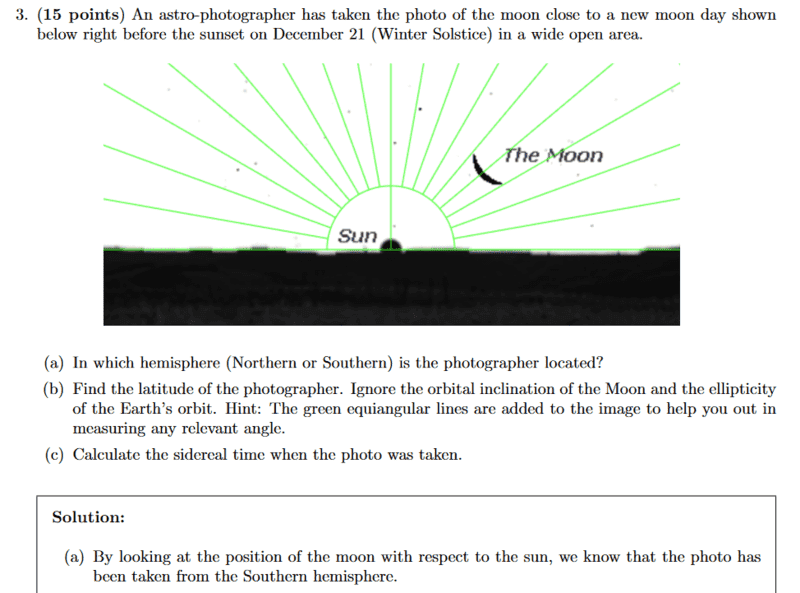
Well this question and answer are really confusing. There are no cardinal directions labelled on the picture. However because the Sun and the Moon should move on a circular path, the left side should be West. This is true for both north and south hemisphere dwellers. What's the reason this is taken by someone living in the southern hemisphere?

 

[Bandersnatch]

the left side should be West.

What do you mean 'left side'? You're looking towards the sunset. The West will be roughly in that direction.

A line drawn between the Moon and the Sun shows you the plane of the ecliptic. The orbit of the Moon is slightly inclined (~5 deg) to it, so it's not exact, but the question lets you ignore it anyway. If you extended that line to form a great circle across the sky, it would be the path the Sun, the Moon, and the planets take through the day (again, ignoring inclinations).
If you are on the Northern hemisphere, you'll see the plane of the ecliptic from 'above'. Conversely on the Southern hemisphere, you see it from 'below'.
Therefore, in the north, when looking to the west, the Moon will be angled to the south - which will be leftwards. In the south, its tilted to the north - to the right of you.

 

[Baluncore]

Based on the ecliptic argument, and personal experience down-under, the observer is clearly in the Southern Hemisphere.

The Sun appears 23.5° deg south at the December solstice, which is the southern summer solstice. Counting from overhead, the ecliptic is 50° degrees down, but 23.5° is due to season, which makes the latitude about 50° - 23° = 27° south.

Sidereal time zero is at high meridian, noon, on the March (vernal) equinox, at zero longitude, (London). The December solstice is 9 months after the March equinox, so the sidereal clock has lagged 24h * 9/12 = 18 hours, plus six hours since noon for the sunset observation, which makes 18 + 6 = 24 = 0 hours. The sidereal time is therefore about zero, but that ignores the fact that at 27° south in summer, the sun sets later than 6 PM, which puts the sidereal time into the early hours of the sidereal morning.

There must be at least one mistake in that reasoning, or maybe two that cancel out.

 

[guv]

I looked at this in Stellarium before posting, unfortunately I was mislead by the pictures without extending ecliptic into an line. Now it's obvious.

 

[guv]

For the 2nd question, looking at their solution, I wonder how they draw the conclusion $\angle K' Sun = 90$ and $\angle K' S Sun = 180$. I came up with this picture. My K is the same as K' (ecliptic pole).The intersections between the Sun's path (slanted dotted path) and the horizon (H) are the sunrise (front) and sunset (back) points. How is $\angle K Sun = 90$? Any line from K to a point on the ecliptic will be perpendicular to the ecliptic, but the Sunset point is not on the ecliptic, it's on the horizon. What's wrong with the picture I draw?

 

[Bandersnatch]

but the Sunset point is not on the ecliptic, it's on the horizon.

The Sun is always on the ecliptic. At sunset, the horizon and the ecliptic intersect where the Sun is.