SUMMARY
The discussion centers on identifying chords of a hyperbola, specifically whether segments AB or PQ qualify as chords. A chord of a hyperbola is defined as any line segment connecting two points on the hyperbola, which can include segments on the same or different branches. The term "focal chord" is mentioned, referring to segments that pass through the focus, particularly the latus rectum. Both AB and PQ can be considered chords in the context provided.
PREREQUISITES
- Understanding of hyperbola geometry
- Familiarity with the concept of chords in conic sections
- Knowledge of focal properties of hyperbolas
- Basic skills in mathematical definitions and terminology
NEXT STEPS
- Research the properties of focal chords in hyperbolas
- Study the definition and characteristics of latus rectum in conic sections
- Explore mathematical texts that cover chords of hyperbolas
- Investigate the differences between chords on the same and different branches of hyperbolas
USEFUL FOR
Students studying conic sections, mathematics educators, and anyone seeking clarity on the properties and definitions related to hyperbolas.
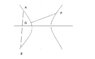
 , but I don't know whether there's general agreement on it.
, but I don't know whether there's general agreement on it.