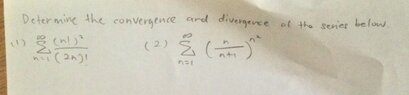Which Test Should I Use: Ratio Test or Root Test in Series Convergence?

Click For Summary
SUMMARY

The discussion clarifies the appropriate use of the Ratio Test and Root Test for determining the convergence or divergence of series in calculus. The Ratio Test is recommended when series terms involve division, such as powers of n or factorials, while the Root Test is suitable for series with terms that can be simplified by taking a root, particularly when "n" is in the exponent. Specific examples illustrate the application of each test, emphasizing the importance of recognizing the structure of the series.

PREREQUISITES
  • Understanding of series convergence and divergence
  • Familiarity with the Ratio Test
  • Knowledge of the Root Test
  • Basic algebraic manipulation skills
NEXT STEPS
  • Study the detailed mechanics of the Ratio Test in calculus
  • Explore the Root Test and its applications in series analysis
  • Practice solving convergence problems using both tests
  • Review examples of series that require different tests for convergence
USEFUL FOR

Students of calculus, mathematics educators, and anyone seeking to deepen their understanding of series convergence techniques.

aruwin
Messages
204
Reaction score
0
Hello.
How do I determine whether to use ratio test or root test in determining whether a series is convergent or divergant? For example, in this problem, ratio is used for no.1 and root test for no.2. Why is that? I need explanation, please.
 

Attachments

  • test.jpeg
    test.jpeg
    7.8 KB · Views: 102
Physics news on Phys.org
aruwin said:
Hello.
How do I determine whether to use ratio test or root test in determining whether a series is convergent or divergant? For example, in this problem, ratio is used for no.1 and root test for no.2. Why is that? I need explanation, please.

If your series has terms that will likely simplify with division (such as powers of n or factorials), then the ratio test is appropriate.

If your series will likely simplify by taking a root (e.g. because it has "n" in the power) then the root test is appropriate.
 
Prove It said:
If your series has terms that will likely simplify with division (such as powers of n or factorials), then the ratio test is appropriate.

If your series will likely simplify by taking a root (e.g. because it has "n" in the power) then the root test is appropriate.

Thank you!
 

Similar threads

Undergrad How does the ratio test fail and the root test succeed here?
  • · Replies 6 ·
Replies
6
Views
4K
MHB Ratio Test Determines Divergence: 11.6.1
  • · Replies 2 ·
Replies
2
Views
2K
MHB 11.6.8 determine convergent or divergence by Ratio Test
  • · Replies 3 ·
Replies
3
Views
2K
Graduate Solving a power series
  • · Replies 3 ·
Replies
3
Views
3K
Undergrad Understanding the nth-term test for Divergence
  • · Replies 17 ·
Replies
17
Views
5K
Undergrad Infinite Series - Divergence of 1/n question
  • · Replies 5 ·
Replies
5
Views
2K
MHB Power Series (Which test can i use to determine divergence at the end points)
  • · Replies 1 ·
Replies
1
Views
2K
MHB Does the Series Converge Absolutely, Conditionally, or Diverge?
  • · Replies 2 ·
Replies
2
Views
2K
MHB Use the techniques of geometric series
  • · Replies 4 ·
Replies
4
Views
2K
Undergrad Does the sequence converge or diverge? (2^n)/(2n)
  • · Replies 9 ·
Replies
9
Views
3K