SUMMARY
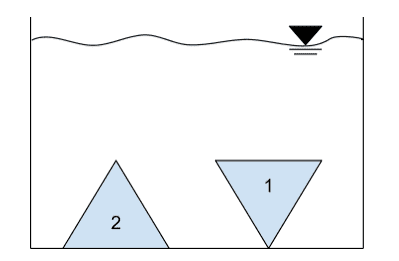
The forum discussion centers on a mechanical aptitude test question regarding the forces exerted on two identical triangles submerged in a water tank. The consensus is that triangle 2 experiences a greater hydrostatic force due to its centroid being deeper than that of triangle 1. Participants highlight the ambiguity in the question, debating whether it refers to net force, hydrostatic force, or the force exerted by the tank's bottom. The discussion emphasizes the importance of clarity in problem statements, particularly in educational contexts.
PREREQUISITES
- Understanding of hydrostatic forces and pressure calculations
- Familiarity with buoyancy principles
- Knowledge of force equilibrium in static systems
- Basic geometry of triangles and centroids
NEXT STEPS
- Research hydrostatic pressure calculations in fluid mechanics
- Study buoyancy and Archimedes' principle in depth
- Explore the concept of force equilibrium in static structures
- Learn about centroid calculations for various geometric shapes
USEFUL FOR
Students preparing for mechanical aptitude tests, educators designing assessment questions, and professionals in engineering and physics fields seeking to clarify concepts of fluid dynamics and force analysis.