User1265
- 29
- 1
- Homework Statement
- Find the current of i1 and i2
- Relevant Equations
- V/R = i
E=V+IR
My attempt at a solution:
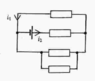
I can see the two resistors at the bottom are in parallel as shown on the circuit diagram attached, but I'm failing to understand why there's a third resistor in parallel.
So I made it one effective resistance as R/2.
Then I proceded to think the circuit short circuits, as Resitor in the middle + R/2 at the bottom has a lower resistance than resistor at the top + middle resistance. So I though i1 = 0 ... I felt like this was wrong and stopped my solution here.
I have been told in order to determine if resistors are in parallel, you must see if the same pd is applied across them, but struggling to see how I can do this here. How do I indentify which are in parallel in this case?
I can see the two resistors at the bottom are in parallel as shown on the circuit diagram attached, but I'm failing to understand why there's a third resistor in parallel.
So I made it one effective resistance as R/2.
Then I proceded to think the circuit short circuits, as Resitor in the middle + R/2 at the bottom has a lower resistance than resistor at the top + middle resistance. So I though i1 = 0 ... I felt like this was wrong and stopped my solution here.
I have been told in order to determine if resistors are in parallel, you must see if the same pd is applied across them, but struggling to see how I can do this here. How do I indentify which are in parallel in this case?