Why do we need to know "two-bands" Hall coefficient and magn

[Philethan]

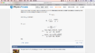
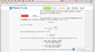
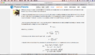
(Oh my god, why can't my post show normally? Some sentences just disappear, but I can still see them while editing. It's very weird. Can someone help me? I've reported.)I know only partially filled bands result in current density, and I think there must be not only 2 partially filled bands, but "several" partially filled bands. For each partially filled band, its Ohm's law is $$\mathbf{E}=\tilde{\rho}_{\text{n}}\:\mathbf{j}_{\text{n}},$$where the $\tilde{\rho}_{\text{n}}$ has the form:$$\tilde{\rho}_n=\begin{pmatrix}\rho_{\text{n}}&-R_{\text{n}}H\\R_{\text{n}}H&\rho_{\text{n}}\end{pmatrix}$$Furthermore, the total induced current is given by$\mathbf{E}=\tilde{\rho}\cdot\mathbf{j}$,with$$\tilde{\rho}=\left(\sum\tilde{\rho}_{\text{n}}^{-1}\right)^{-1}$$In Ashcroft & Mermin Solid State Physics textbook, it's said the Hall coefficient and magnetoresistance by only two bands are:$$R=\frac{R_1\rho_2^2+R_2\rho_1^2+R_1R_2(R_1+R_2)H^2}{(\rho_1+\rho_2)^2+(R_1+R_2)^2H^2}$$$$\rho=\frac{\rho_1\rho_2(\rho_1+\rho_2)+(\rho_1R_2^2+\rho_2R_1^2)H^2}{(\rho_1+\rho_2)^2+(R_1+R_2)^2H^2}$$Why do we need these two formulas if it's almost impossible to have only two partially filled bands? Thank you very much!

 

[berkeman]

Your post looks fine. Try refreshing your browser -- does it look okay now? If not, we will try to help.

 

[Philethan]

Your post looks fine. Try refreshing your browser -- does it look okay now? If not, we will try to help.

Thanks so much. I found it doesn't show normally in Safari, but it's good in Chrome. Please help me check if there's something wrong with backend settings. Thank you so much :D Here's my screenshots.

It's Safari:

And it's Chrome:

Thank you so much!------------[Update]------------It works in Safari now. It's weird... Anyway, thanks :)