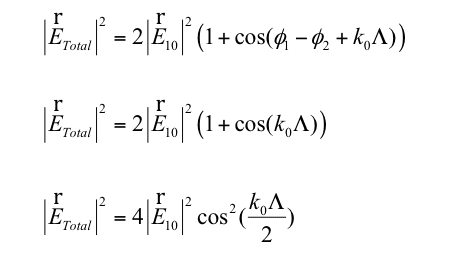Discussion Overview
The discussion revolves around the mathematical relationship between the cosine functions in the context of wave interference, specifically examining the equation cos(φ1 - φ2 + kx) = cos(kx). Participants explore the implications of phase differences and conditions under which this equality holds, focusing on theoretical aspects of wave behavior.
Discussion Character
- Exploratory, Technical explanation, Debate/contested
Main Points Raised
- One participant suggests that the equality cos(φ1 - φ2 + kx) = cos(kx) may be a result of algebraic manipulation related to path differences in wave interference.
- Another participant notes that the equality could hold true if φ1 - φ2 is a multiple of 2π, indicating a condition for the relationship.
- A different viewpoint introduces the assumption of equal phase velocities for the waves, leading to the conclusion that φ1 = φ2, which may simplify the situation.
- One participant questions whether φ is defined as ωt, seeking clarification on the variables involved.
- Another participant argues against this definition, suggesting that φ is distinct from ωt, as φ is used in the context of defining wave amplitude.
- A later reply introduces a specific example of two plane waves interfering, asking for clarification on the context of the discussion.
Areas of Agreement / Disagreement
Participants express differing views on the conditions under which the equality holds, with no consensus reached regarding the definitions and implications of the variables involved.
Contextual Notes
There are unresolved assumptions regarding the definitions of φ1, φ2, and their relationship to the wave parameters, as well as the specific context of the wave interference being discussed.