nghijen
- 2
- 0
I have attempted to solve the question but I still do not understand. Can someone please help me?
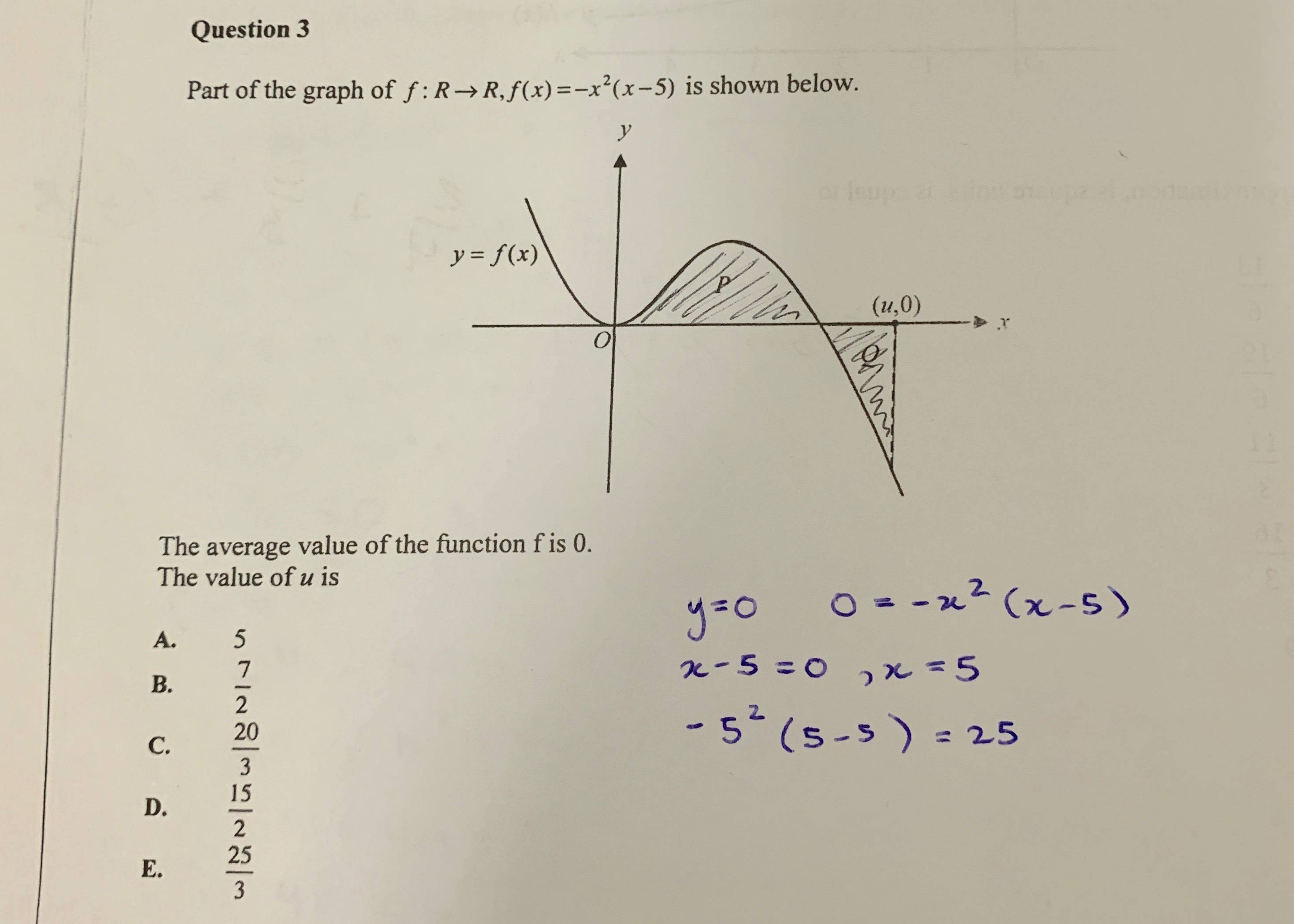
The discussion centers on the calculation of the average value of a function using definite integrals, specifically the function \( f(x) = x^2(5-x) \) over the interval \([0, u]\). The average value is defined as \(\frac{1}{u-0} \int_0^u f(x) \, dx\). Participants highlight the importance of correctly identifying the interval and performing the integration, noting that the average value formula requires proper execution of the integral. Miscalculations, such as incorrectly evaluating \( -5^2(5-5) \), lead to confusion regarding the function's roots.
PREREQUISITESStudents learning calculus, educators teaching integration concepts, and anyone seeking to understand the average value of functions through definite integrals.
skeeter said:average value of a function involves a definite integral over an interval ... from your shading, is the given interval $[0,u]$ ?
nghijen said:I am assuming it is [0, u] !