Why Does My Calculation Differ from the Textbook's Answer?

[bcjochim07]

Homework Statement

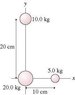
Find the total gravitational potential energy of the three masses.

Homework Equations

U=-GMm/r

The Attempt at a Solution

U between the 10 kg mass & the 20kg mass
-(6.67*10^-11)(20kg)(10kg)/.20 m = -6.67 * 10 ^-8 J

U between the 20kg mass and the 5 kg mass
-(6.67*10^-11)(20kg)(5kg)/.10m = -6.67*10^-8 J

U between the 10 kg mass & the 5 kg mass
-(6.67*10^-11)(10kg)(5kg)/.2236 m = -1.49 * 10^-8 J

adding them up I got -1.483*10^-7 J

but the back of my book says -1.96 * 10^-7 J

Am I doing something wrong?

 

[alphysicist]

Hi bcjochim07,

The image file is not ready to view. Is it simple enough to describe in words?

 

[bcjochim07]

A 10 kg mass is located 20 cm directly above a 20 kg mass. And 10 cm to the right of the 20kg mass is a 5kg mass. The masses form a right angle

 

[alphysicist]

Your answer looks right to me.