unscientific
- 1,728
- 13
In this section, they derive the Sommerfeld formula.
In the first step it seems like they have expanded ##\frac{1}{(1+e^x))^2}##. I'm not sure why does the series taylor expand as ##e^{-nx}##?
Also how did they get from the 2nd to the 3rd step?
Simply by comparing terms we see they are different:
For 2nd step we get terms of ##x^se^x(-1 + 2e^{-x} - 3e^{-2x} + ...)##.
For 3rd step we get terms of ##e^{-x} - 2e^{-2x} + 3e^{-3x} - ...##
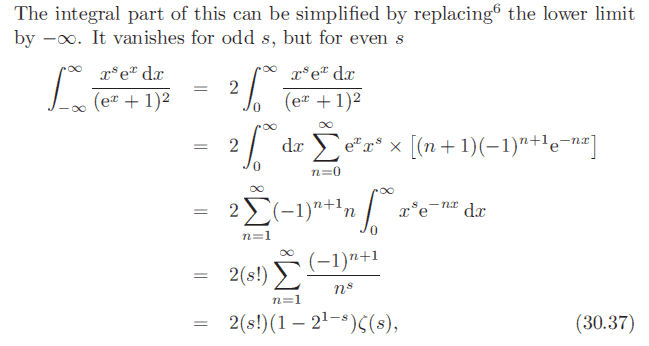
In the first step it seems like they have expanded ##\frac{1}{(1+e^x))^2}##. I'm not sure why does the series taylor expand as ##e^{-nx}##?
Also how did they get from the 2nd to the 3rd step?
Simply by comparing terms we see they are different:
For 2nd step we get terms of ##x^se^x(-1 + 2e^{-x} - 3e^{-2x} + ...)##.
For 3rd step we get terms of ##e^{-x} - 2e^{-2x} + 3e^{-3x} - ...##