Why Does This Equation Include Sums of h(t-ti)? Explained.

[paalfis]

Can someone explain to me why in this equation (attached)

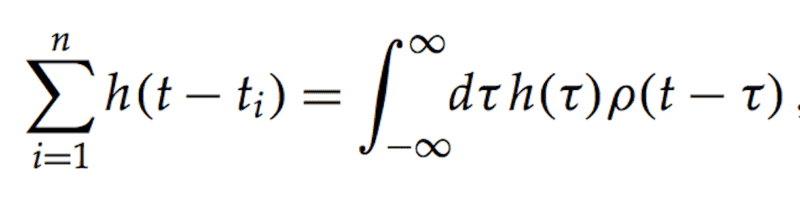
where ρ(t)=$\sum$δ(t-ti) , dirac funtion.
in the left side we have the sum over h(t-ti) instead of the sum over h(ti) ?

It seems to me that the integral would work summing 1*h(t1)+1*h(t2)+...+1*h(ti) for all ti smaller than t.

 

[Fredrik]

$$\int\mathrm d\tau\, h(\tau)\rho(t-\tau) =\int\mathrm d\tau\, h(\tau)\sum_i\delta((t-\tau)-t_i) =\sum_i\int\mathrm d\tau\, h(\tau)\delta(\tau-(t-t_i)) =\sum_i h(t-t_i)$$

 

[paalfis]

Thanks, one more question, what does tau stands for in this type of integral. i.e. What is the meaning of (t-tau)?

 

[Fredrik]

It's a dummy variable (i.e. it can be replaced by any other variable symbol), so it's not really significant. But since you plug it into the same functions where you plug in $t$ and $t_i$, it can be thought of as representing the same sort of thing as those guys do. (For example, time or temperature, or whatever t stands for in this context). This is especially clear when you approximate an integral by a Riemann sum, $\int f(x)\mathrm dx\approx\sum_i f(x_i)(x_{i+1}-x_i)$.