SUMMARY
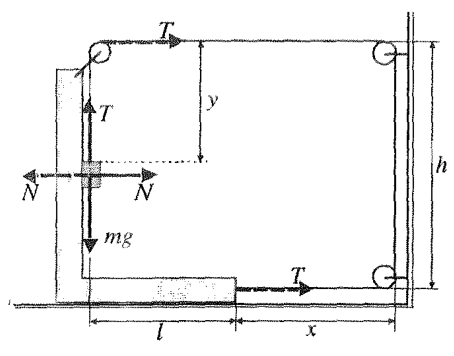
The discussion focuses on the relationship between the displacements in a pulley system, specifically why 2Δx = Δy. Participants emphasize the importance of visualizing the setup and identifying which segments of the rope change length when the system is altered by Δx. They highlight that some pulleys function solely to change the direction of the rope, while others reduce the effort required to lift a load, effectively doubling the length of rope needed to achieve a certain vertical displacement.
PREREQUISITES
- Understanding of basic pulley mechanics
- Familiarity with displacement notation (Δx and Δy)
- Knowledge of vector directionality in physics
- Ability to draw and interpret free-body diagrams
NEXT STEPS
- Study the mechanics of different types of pulleys
- Learn how to draw and analyze free-body diagrams in pulley systems
- Explore the principles of mechanical advantage in simple machines
- Investigate the role of tension in rope systems
USEFUL FOR
Students preparing for physics competitions, educators teaching mechanics, and anyone interested in understanding the dynamics of pulley systems.
 !
!