Homework Help Overview
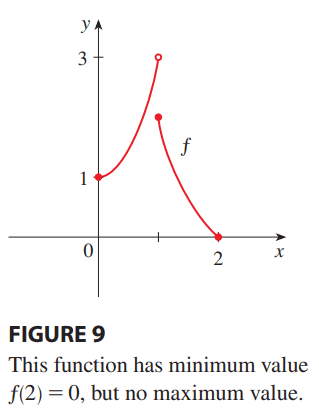
The discussion revolves around the necessity of continuity for applying the Extreme Value Theorem in the context of a function's maximum value. Participants are exploring why certain values cannot be considered as absolute maxima without the theorem's conditions being met.
Discussion Character
- Conceptual clarification, Assumption checking
Approaches and Questions Raised
- Participants question the validity of assuming a function's value at points approaching a boundary and whether those points can be considered in determining maximum values. There is discussion about the implications of continuity and the nature of supremum versus maximum.
Discussion Status
The conversation is actively exploring the conditions under which the Extreme Value Theorem applies, with some participants providing clarifications about continuity and domain restrictions. There is no explicit consensus, but productive questions and corrections are being raised.
Contextual Notes
Participants note that the function in question is discontinuous at certain points, which affects the applicability of the Extreme Value Theorem. The discussion highlights the importance of understanding the definitions and properties of the function involved.
