Why Is Instantaneous Velocity Equal to Average Velocity?

[urapeach]

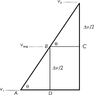
Does anyone happen to know why the instantaneous velocity at the midpoint of a time interval is equal to the average velocity over the same time interval?? I can't seem to prove this reasoning.

Thanks!

 

[russ_watters]

You're talking about when acceleration is constant... It's just from the definition of "average" - the 2 in the denominator is where you get the halfway point in time.

 

[andrevdh]

First note that the average velocity is midway between the two velocities values, $v_1,\ v_2$, at the endpoints of the interval. Since
$$v_1+\frac{1}{2}(v_2-v_1)=v_1+\frac{v_2}{2}-\frac{v_1}{2}$$

$$=\frac{v_1+v_2}{2}$$
We therefore need to show that the time at which the average velocity is reached is in the middle of the time interval. In the drawing time is on the horizontal x-axis and speed on the vertical y-axis. What needs to be proved then in the drawing is that $AD=BC$, It is clear that both these length are given by
$$\frac{\Delta v}{2\tan(\theta)}$$