Why is my simulation of projectile trajectory with air resistance wrong?

[fisicist]

Hey!

This started very harmless... A friend and I were throwing stones in a lake. Mine didn't get very far, he was teasing me "What was the ideal angle again?". Of course, I know it should be 45°. I replied in jest: "That's because I'm considering air resistance!" Then we had a discussion what the ideal angle should be with air resistance considered.
So I wrote a simulation in Python. It was just for fun... But I encountered an issue that I don't quite understand: The simulated trajectory is wrong. I hope someone can help me understand where this is coming from, and perhaps give me some hint how to fix it.

My code is:
[CODE lang="python" highlight="11-17, 33,34, 23, 25-27"]import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

c = 7
v = 5

# f gives phase space velocity
# z = [x, y, v_x, v_y]
# f(t, z) = [v_x, v_y, a_x, a_y]
def f(t, z):
global c
vel = z[2:]
friction = -c * np.absolute(vel) * vel
gravity = [0, -0.5]
accel = friction + gravity
return np.concatenate((vel, accel))

def hit_ground(t, z): return z[1]
hit_ground.terminal = True
hit_ground.direction = -1

t_eval = np.linspace(0, 100, 10000)

def v_init(theta):
global v
return v * np.array([np.cos(theta), np.sin(theta)])

thetas = np.linspace(0.0, np.pi/2, 181)
dists = np.array([])
plt.subplot('211')
for counter,theta in enumerate(thetas):
init = np.concatenate((np.array([0., 0.]), v_init(theta)))
sol = solve_ivp(f, [0, 100], init, t_eval = t_eval, events=hit_ground)
if counter % 40 == 0:
plt.plot(sol.y[0,:], sol.y[1,:], label='{:4.0f} °'.format(theta*180/np.pi))
plt.gca().quiver(sol.y[0,::70], sol.y[1,::70], 1000*sol.y[2,::70], 1000*sol.y[3,::70])
dists = np.append(dists, [sol.y[0,-1]])
#plt.gca().set_aspect('equal', adjustable='box')
plt.legend(loc='upper left')
plt.xlabel('$x$')
plt.ylabel('$y$')

plt.subplot('212')
plt.plot(thetas*180/np.pi, dists, 'r-')
best_angle = thetas[np.argmax(dists)]
plt.gca().axvline(x = best_angle*180/ np.pi)
print('{:3.1f}'.format(best_angle*180/ np.pi))
plt.xlabel('angle [°]')
plt.ylabel('distance')

plt.show()
[/CODE]

Result:

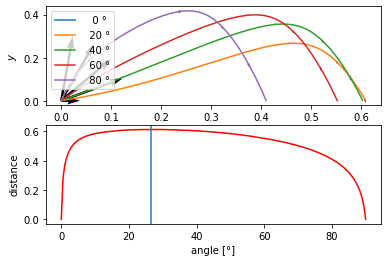
This shouldn't happen... As you can see, the curves bend upward, i.e. are not concave. Even without knowing the exact solution y(x), it is easy to prove it should be a concave function.
The model is \ddot{x} = - c \dot{x}\sqrt{\dot{x}^2+\dot{y}^2}, \ddot{y} = - c \dot{y} \sqrt{\dot{x}^2+\dot{y}^2} - \frac 1 2
By the chain rule, \frac{d^2 y}{d^2 x} (x(t)) = \frac{\ddot{y}}{\dot{x}^2} - \dot{y}\frac{\ddot{x}}{\dot{x}^3} = \frac{1}{\dot{x}^2} \left( -2 c \dot y \sqrt{\dot{x}^2+\dot{y}^2} - \frac 1 2 \right)
Therefore, at least as long as \dot{y} \geq 0, this should be a concave function. If I through it downwards with high speed, it might get convex there, but not as long as the motion is upward.
CORRECTION: By the chain rule: \frac{d^2 y}{d^2 x} (x(t)) = -\frac{1}{2 \dot{x}^2} \leq 0

So, what is wrong with the simulation? I know the time subdivision is not very high. But that shouldn't matter, because also in the discretized model, the velocity vector should be shortened and then get a downward contribution in every step. That's not what I see in the plot.

Any ideas, anyone?

 

[Dale]

Therefore, at least as long as \dot{y} \geq 0, this should be a concave function.

Hmm, I am not seeing that, where do you get that condition from?

 

[fisicist]

Hmm, I am not seeing that, where do you get that condition from?

1/\dot{x}^2 \geq 0 manifestly, so it remains to check that -2 c \dot{y} \sqrt{\dot{x}^2+\dot{y}^2}-\frac 1 2 \leq 0 in order for d^2 y/ d x^2 \leq 0 (i.e. concavity). But -2 c \sqrt{\dot{x}^2 +\dot{y}^2} is always negative, so if \dot{y} \geq 0, everything is negative.

 

[Dale]

What about the 1/2?

 

[A.T.]

Hmm, I am not seeing that, where do you get that condition from?

An informal argument for concavity: The drag is always tangential so it doesn't change the direction, while gravity is always bending the path down.

Looks like some lift sneaked in somewhere.

 

[fisicist]

Hey sorry, I've made a sign error. The two friction terms compensate each other, not add up. Actually not surprising: Without gravity, motion is along a straight line.
I will correct it. Correct is
d^2 y / dx^2 = - \frac{1}{2 \dot{x}^2}
Still, it's concave. In fact, it is *always* concave, even if I throw the stone downwards.

 

[A.T.]

As you can see, the curves bend upward, i.e. are not concave.

I would call bending upward and then downward "concave". Bending only downward would be "convex", and what you would expect here.

Have you tried coding a simple Euler integration yourself?

 

[fisicist]

I would call bending upward and then downward "concave". Bending only downward would be "convex", and what you would expect here.

Have you tried coding a simple Euler integration yourself?

The standard definition used in mathematics (in fields such as calculus of variations, 'convex analysis' or 'convex optimization') is that a function is convex if its epigraph \operatorname{epi}f := \lbrace (x, y) : y \geq f(x) \rbrace is a convex set. For a twice differentiable function, this is equivalent to f'' \geq 0. A function f is concave if -f is convex.

 

[A.T.]

The standard definition used in mathematics (in fields such as calculus of variations, 'convex analysis' or 'convex optimization') is that a function is convex if its epigraph \operatorname{epi}f := \lbrace (x, y) : y \geq f(x) \rbrace is a convex set. For a twice differentiable function, this is equivalent to f'' \geq 0. A function f is concave if -f is convex.

Ok, thanks. I would suggest coding a simple Euler integration. It should never bend upwards.

 

[fisicist]

Thank you to everyone who replied here!
I found the error. It's not a mathematical or numerical curiosity, but a simple coding error. Namely,

np.absolute(vel)

does not give \vert \dot{\mathbf x} = \sqrt{\dot{x}^2+\dot{y}^2}, as I thought it would, but (\vert \dot x \vert, \vert \dot y \vert )^T, and

np.absolute(vel) * vel

does not give \dot{\mathbf{x}} \vert \dot{\mathbf{x}} \vert, as I thought it would, but (\dot{x} \vert \dot{x} \vert, \dot{y} \vert \dot{y} \vert )^T.

The correct way to do it is

np.sqrt(vel.dot(vel)) * vel

 

[William Crawford]

Thank you to everyone who replied here!
I found the error. It's not a mathematical or numerical curiosity, but a simple coding error. Namely,

np.absolute(vel)

does not give \vert \dot{\mathbf x} = \sqrt{\dot{x}^2+\dot{y}^2}, as I thought it would, but (\vert \dot x \vert, \vert \dot y \vert )^T, and

np.absolute(vel) * vel

does not give \dot{\mathbf{x}} \vert \dot{\mathbf{x}} \vert, as I thought it would, but (\dot{x} \vert \dot{x} \vert, \dot{y} \vert \dot{y} \vert )^T.

The correct way to do it is

np.sqrt(vel.dot(vel)) * vel

Congratulation! So what is the ideal angle when you include air resistance?

 

[fisicist]

For anyone interested in the physics: Qualitatively, the result is similar.

Qualitatively, the best angle decreases rapidly the higher the friction is:

 

[Herman Trivilino]

Run your sim on a baseball and see if 40 deg gives the maximum range.

 

[A.T.]

The correct way to do it is

np.sqrt(vel.dot(vel)) * vel

Or:

np.linalg.norm(vel) * vel

https://docs.scipy.org/doc/numpy/reference/generated/numpy.linalg.norm.html

For anyone interested in the physics: Qualitatively, the result is similar.
View attachment 247485
Qualitatively, the best angle decreases rapidly the higher the friction is:
View attachment 247487

Regarding your stone throwing contest:

You could plot the optimal angle as function of the object's density for a given realistic object shape/size and throw speed. It could be that for stones the angle is pretty close to 45° at the speed you can throw, while for light balls (like tennis) it makes sense to aim lower.

Bio-mechanics complicates matters because you won't achieve the same throw speeds for any angle.

Finally, your friend might simply throw much faster, and thus further, even at sub optimal angles.