member 731016
Hi!
For this part (e) of this problem,

Source: https://ocw.mit.edu/courses/8-01sc-...647ea989a352a972dc4b3dfe_MIT8_01F16_pset7.pdf
The solutions are,
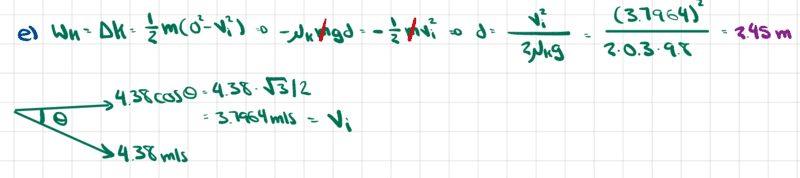
However, I don't understand why they only used a component of the initial velocity as it comes off the incline. I used 4.38 m/s because I thought that once the block reaches the horizontal surface, the vertical and horizontal components of the velocity from the incline would combine to give 4.38 m/s. Do you please know why or whether the solutions are wrong?
Many thanks!
For this part (e) of this problem,
Source: https://ocw.mit.edu/courses/8-01sc-...647ea989a352a972dc4b3dfe_MIT8_01F16_pset7.pdf
The solutions are,
However, I don't understand why they only used a component of the initial velocity as it comes off the incline. I used 4.38 m/s because I thought that once the block reaches the horizontal surface, the vertical and horizontal components of the velocity from the incline would combine to give 4.38 m/s. Do you please know why or whether the solutions are wrong?
Many thanks!