jasonpeng
- 19
- 0
I've got a problem with understanding the pulley system.
In a basic pulley, if the force pulling M upwards is T, and the force pulling m upwards is also T, why is it that T is equal for both m & M? For some reason I feel inclined to believe that the T pulling m upwards is equal to the weight of M, and the T pulling M upwards is equal to the weight of m. Is that right or wrong? Why?
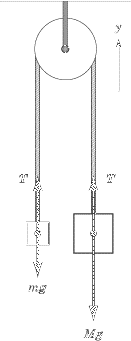
In a basic pulley, if the force pulling M upwards is T, and the force pulling m upwards is also T, why is it that T is equal for both m & M? For some reason I feel inclined to believe that the T pulling m upwards is equal to the weight of M, and the T pulling M upwards is equal to the weight of m. Is that right or wrong? Why?