arhzz
- 284
- 58
- Homework Statement
- Find the Fourier coefficients
- Relevant Equations
- Fourier Analysis
Hello!
I have a function that is periodic. T = 2. Now I need to find a fourier series of that function, so I need to find coefficient ##a_0 a_k b_k ##
for a0 I have this formula (this is the one we used in class)
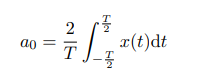
Now my x(t) = (-t+1). and when I plug in all of the values I have in the formula I get that ##a_0 = 2 ## but the solution says it should be 1. I checked the solution and what they did is they multiplied the 2/T with 2. I dont understand why they did this? Also they integrated from 0 to 1, I dont understand this either; Shouldnt the Integral be from -1 to 1 ?
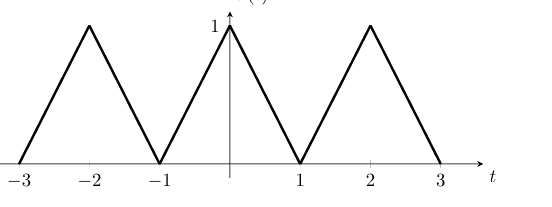
For reference here is how the graph of the function looks like.
Thanks in advance!
I have a function that is periodic. T = 2. Now I need to find a fourier series of that function, so I need to find coefficient ##a_0 a_k b_k ##
for a0 I have this formula (this is the one we used in class)
Now my x(t) = (-t+1). and when I plug in all of the values I have in the formula I get that ##a_0 = 2 ## but the solution says it should be 1. I checked the solution and what they did is they multiplied the 2/T with 2. I dont understand why they did this? Also they integrated from 0 to 1, I dont understand this either; Shouldnt the Integral be from -1 to 1 ?
For reference here is how the graph of the function looks like.
Thanks in advance!