Rikudo
- 120
- 26
- Homework Statement
- A chain with length L is held stretched out on a frictionless horizontal
table, with a length y0 hanging down through a hole in the table. The
chain is released. As a function of time, find the length that hangs down
through the hole (don’t bother with t after the chain loses contact with
the table).
- Relevant Equations
- F = dp/dt
Firstly, There is something I want to clarify. When the system starts moving, parts of the chain that still lies on the table, which have mass
## \frac {(L- y_0)M} {L}##, will be pulled by the force that the hanging chain's weight exert,right?
If yes, then :
As far as I know, the formula ##F= ma## is originally created from ##F= m\,\frac {dv} {dt} + v\, \frac {dm}{dt}##, which can be used only if there is no change in mass.
So, as I have stated in the first paragraph, the mass that is pulled by hanging chain will continue to change after the system starts moving. Then, why the book still use ##F = ma## although the mass is not constant?
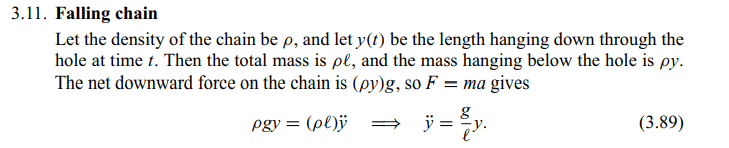
## \frac {(L- y_0)M} {L}##, will be pulled by the force that the hanging chain's weight exert,right?
If yes, then :
As far as I know, the formula ##F= ma## is originally created from ##F= m\,\frac {dv} {dt} + v\, \frac {dm}{dt}##, which can be used only if there is no change in mass.
So, as I have stated in the first paragraph, the mass that is pulled by hanging chain will continue to change after the system starts moving. Then, why the book still use ##F = ma## although the mass is not constant?