SUMMARY
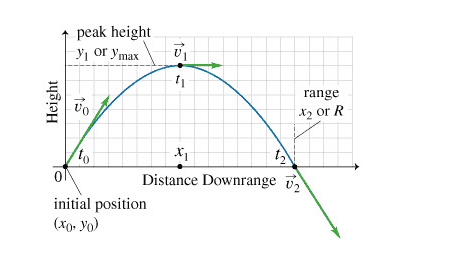
The acceleration due to gravity is consistently represented as -9.8 m/s² when using a coordinate system that defines upward as positive. This is because gravity acts downward, leading to a negative acceleration in the upward direction. The discussion clarifies that while an object moves upward, its vertical velocity decreases until it reaches zero, indicating deceleration. Conversely, during descent, the vertical velocity increases, confirming that the acceleration is positive in the downward direction.
PREREQUISITES
- Understanding of basic physics concepts, specifically Newton's laws of motion.
- Familiarity with vector components and sign conventions in physics.
- Knowledge of kinematic equations, particularly SUVAT equations.
- Basic grasp of projectile motion and its characteristics.
NEXT STEPS
- Study the derivation and application of SUVAT equations in various motion scenarios.
- Learn about the effects of air resistance on projectile motion and how it alters acceleration.
- Explore different coordinate systems and their implications on vector representation in physics.
- Investigate the concept of resultant forces and their relationship to acceleration in various contexts.
USEFUL FOR
Students of physics, educators teaching kinematics, and anyone interested in understanding the principles of motion and acceleration in a gravitational field.