Work Done by Gravity on Box on Ice Arc - Radius 8m, Angle 14 Degrees

[BlasterV]

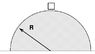
A perfect hemisphere of frictionless ice has radius R = 8 meters. Sitting on the top of the ice, motionless, is a box of mass m = 10 kg.

The box starts to slide to the right, down the sloping surface of the ice. After it has moved by an angle 14 degrees from the top, how much work has gravity done on the box?

Ok I did W = Arc length * Gravitation force
W = ((14 / 360)2PI*8m )( 9.8 m/s^2 * 10 kg )

Can someone tell me what I'm doing wrong here? Thanks. I have attached a GIF

How fast is the box moving?
Once part one is right, this is easy, since W = 10kgV^2. The problem is finding part one.

 

[Justin Lazear]

Do you remember the definition of work?

W = \int \vec{F} \cdot d\vec{r}

Work is only done in the direction of motion, and gravity is not always acting in the direction of motion.

--J

 

[BlasterV]

That doesn't tell me much, how do I find force in the direction of motion then with a surface that is sloping like that?

 

[Parth Dave]

Gravity always works in one direction: downwards.

 

[Bartholomew]

Also, the box turns as it slides so you can't use the formula for energy to find the speed directly. Some of the box's energy goes into turning, not forward motion.

 

[Justin Lazear]

That doesn't tell me much, how do I find force in the direction of motion then with a surface that is sloping like that?

Of course you know the direction of motion! The box isn't magically going to fall through the hemisphere, nor is it going to magically going to fly off of it! It's going to follow the surface of the hemisphere exactly.

So at any given point on the hemisphere, which way is the box moving?

--J

 

[BlasterT]

BlasterV

Are you mentally challenged BlasterV?