Work/energy - spring and inclined plane

[shawli]

Homework Statement

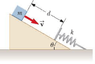
An inclined plane of angle 20.0° has a spring force constant k = 500 N/m fastened securely at the bottom so that the spring is parallel to the surface (as shown in the attached photo). A block of mass m = 2.50kg is placed on the plane at a distance d = 0.300m from the spring. From this position, the block is projected towards the spring with speed v = 0.750m/s. By what distance is the spring compressed when the block momentarily comes to rest?

Homework Equations

K = 1/2 m * v²

E_elastic = E_s = 1/2 k * x²

E_g = mgh

The Attempt at a Solution

I get a bit confused when handling all the different Energy/Work equations...
But here's what I did:
(my variable "x" is the distance that the spring displaces, and I tried to set my coordinate system so that the x-axis would be where the spring is at its compressed position but I'm not sure if I did it properly...)

U_gi + U_si + K_i = U_gf + U_sf + K_f
(2.50)(9.80)(0.300 + x)sin20 + 0 + 1/2*2.50*0.750² = 0 + 1/2 * 500 * x² + 0

However when I solve for x, I get the wrong value.

I think I may have set up my equations for gravitational potential energy incorrectly ... Or maybe I set the whole thing up wrong heh.

 

[PhanthomJay]

Looks perfect to me! ...maybe your math is off...recheck your numbers...

 

[shawli]

Bah, you're right, I had calculation errors -_-

But yay, that means I got it! Thanks for checking :)