Work of Varying X Component by Integration

[Ad Astra]

Homework Statement

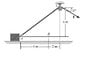
A 76-kg crate starts from rest at A and is moving at 8 m/s. Using integration, find the work done between A and B of the variable x component of force F= 756 N. (See attached jpeg for the geometry of the problem)

EDIT: We are doing a variation of the problem shown in the jpeg below, the only difference being the length from A to B (5 m instead of 6 m) and the vertical position of the pulley (5 m instead of 6 m).

Homework Equations

U_1-2= ∫F cos θ dx

The Attempt at a Solution

Since F is constant and cos θ is variable, I've tried to relate cos θ in terms of the displacement in x. Since cos θ = Δx/Δ(Length of rope), and because the vertical displacement of the pulley remains constant (5 m), I obtained a value of:

cos θ = x/(x² + 25)^-1/2

Whenever I solve this integral I end up with a value equal to the magnitude of the force multiplied by a displacement of 7.5 m in x which, from the geometry of the problem, is impossible. Obviously, I'm just not looking at this correctly. Any hints would be very helpful, and thank you in advance.

 

[Doc Al]

Since F is constant and cos θ is variable, I've tried to relate cos θ in terms of the displacement in x. Since cos θ = Δx/Δ(Length of rope), and because the vertical displacement of the pulley remains constant (5 m), I obtained a value of:

cos θ = x/(x² + 25)^-1/2

Looks good. (Except for the minus sign in front of the 1/2. I assume that was a typo.)

Whenever I solve this integral I end up with a value equal to the magnitude of the force multiplied by a displacement of 7.5 m in x which, from the geometry of the problem, is impossible.

What did you get when you integrated? What were your limits of integration?

 

[Ad Astra]

∫_0m^5m (F cos θ) dx

= F∫_0m^5m (cos θ) dx

= F∫_0m^5m [x(x² + 25)^-1/2] dx

= F∫_0m^5m [1 + (x/5)] dx

= F{∫_0m^5m dx + 1/5∫_0m^5m x dx}

= F{[x + x²/10]^5m_0m}

= F{[(5 m) + (5 m)²/10] - [0]}

= F(7.5 m), where F= 756 N

= 5670 J

This just seems to be too high a value to me. Since the x component of F is always decreasing and can never be more than F itself and, furthermore, is not applied for a displacement greater than 5 m, I feel this value should be lower than this. Maybe I'm wrong, but I can't figure out where it is exactly that I'm going wrong.

Sorry if my notation seems a little sloppy, I've never tried to express an integral via digital media before. I hope it makes sense.

 

[Doc Al]

∫_0m^5m (F cos θ) dx

= F∫_0m^5m (cos θ) dx

= F∫_0m^5m [x(x² + 25)^-1/2] dx

OK. Are the limits 0 to 5 or 2 to 7?

= F∫_0m^5m [1 + (x/5)] dx

How did you get this?

 

[Ad Astra]

OK. Are the limits 0 to 5 or 2 to 7?


How did you get this?

I wish there was an emoticon for an embarrassed slap to one's own forehead. I can't believe I made such an amateurish move. I guess I somehow convinced myself that (a + b)^x was equal to a^x + b^x and then multiplied both terms by x. I was just trying to simplify my integral before trying to integrate.

Now I feel better for knowing where I was going wrong, but am left with the task of integrating the square root of a sum of squares. I don't even know where to begin on that one. Maybe some sort of trig substitution?

My teacher said that it was fairly simple integral and now I feel like a moron for not being able to grasp it. I feel like the answer is right there in front of me and I'm just not seeing it...

EDIT: The upper limits are from A to B (in the picture I provided), or from 0m to 5 m so far as I can tell.

 

[Doc Al]

Now I feel better for knowing where I was going wrong, but am left with the task of integrating the square root of a sum of squares. I don't even know where to begin on that one. Maybe some sort of trig substitution?

Nah, nothing that complicated.

You need to find the antiderivative of \frac{x}{\sqrt{x^2 + a^2}}

Play around with it a bit. (Or just look it up!)

EDIT: The upper limits are from A to B (in the picture I provided), or from 0m to 5 m so far as I can tell.

In your diagram, B is not directly under C.