francisco300
- 9
- 0
Work Problem -- Pushing a lawnmower
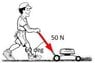
1. A lawn mower (25kg) is pushed a horizontal distance of 10m by a 50 N downward force directed 60 degrees to the horizontal. The coefficient of kinetic frictional force is .017. What is the work done by each of the external forces on the lawn mower?
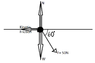
3. So basically I start off every problem by drawing a free body diagram. I label each force and its direction. I know there is Normal force going up, its Weight going down, and I believe a force going 60 degrees below the horizontal in what would be quadrant 4.
The part I need help in is friction. If you push on a lawn mower the wheels turn clockwise meaning kinetic friction would be pushing right? (This is assuming you picture the lawn mower is being pushed from left to right as is my diagram) I am confused because my instructor did a similar problem where friction was going left which is not opposite of how the wheel turns.
1. A lawn mower (25kg) is pushed a horizontal distance of 10m by a 50 N downward force directed 60 degrees to the horizontal. The coefficient of kinetic frictional force is .017. What is the work done by each of the external forces on the lawn mower?
Homework Equations
3. So basically I start off every problem by drawing a free body diagram. I label each force and its direction. I know there is Normal force going up, its Weight going down, and I believe a force going 60 degrees below the horizontal in what would be quadrant 4.
The part I need help in is friction. If you push on a lawn mower the wheels turn clockwise meaning kinetic friction would be pushing right? (This is assuming you picture the lawn mower is being pushed from left to right as is my diagram) I am confused because my instructor did a similar problem where friction was going left which is not opposite of how the wheel turns.
Last edited by a moderator: