- #1
Tom Hardy
- 46
- 1
Here is some background to the problem (in a stirred tank):
"With yield stress non-Newtonian (viscoplastic) fluids, it is possible to generate an agitated volume around the impeller, defined as a cavern, surrounded by a stagnant region where the shear stress is insufficient to overcome the apparent yield stress of the fluid."
Sometimes you can get a cylindrical cavern around the impeller, see the below image.
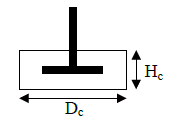
"By performing a force balance between the applied torque, Γ and the shear stress acting on the surface of a cylinder, we can define the boundary by setting the shear stress equal to the yield stress τ = τY. The total torque is given by:
$$\Gamma = \frac{\pi}{2} \tau_{y}H_{C}D_{C}^2+\frac{\pi}{6}\tau_{y}D_{C}^3$$
I just can't get the second term. The first term I can get by doing:
$$\Gamma_{1}=\tau_y \cdot Area_{Curved} \cdot \frac{D}{2} = \pi \cdot \frac{D^2}{2} \cdot H_{c} \cdot \tau_{y}$$
This gets me the first term...but the second term I just can't get, this is what I'm doing:
$$\Gamma_{2}=\tau_{y} \cdot Area_{Faces} \cdot \frac{D}{2} =\tau_{y} \cdot 2 \pi \cdot \frac{D^2}{4} \cdot \frac{D}{2} = \tau_{y} \cdot \pi \cdot \frac{D^3}{4} $$
Argh, so I'm getting D^2/4 instead of D^2/6 for the second term and I just can't work it out, if anyone can help I'd appreciate it. Thanks.
"With yield stress non-Newtonian (viscoplastic) fluids, it is possible to generate an agitated volume around the impeller, defined as a cavern, surrounded by a stagnant region where the shear stress is insufficient to overcome the apparent yield stress of the fluid."
Sometimes you can get a cylindrical cavern around the impeller, see the below image.
"By performing a force balance between the applied torque, Γ and the shear stress acting on the surface of a cylinder, we can define the boundary by setting the shear stress equal to the yield stress τ = τY. The total torque is given by:
$$\Gamma = \frac{\pi}{2} \tau_{y}H_{C}D_{C}^2+\frac{\pi}{6}\tau_{y}D_{C}^3$$
I just can't get the second term. The first term I can get by doing:
$$\Gamma_{1}=\tau_y \cdot Area_{Curved} \cdot \frac{D}{2} = \pi \cdot \frac{D^2}{2} \cdot H_{c} \cdot \tau_{y}$$
This gets me the first term...but the second term I just can't get, this is what I'm doing:
$$\Gamma_{2}=\tau_{y} \cdot Area_{Faces} \cdot \frac{D}{2} =\tau_{y} \cdot 2 \pi \cdot \frac{D^2}{4} \cdot \frac{D}{2} = \tau_{y} \cdot \pi \cdot \frac{D^3}{4} $$
Argh, so I'm getting D^2/4 instead of D^2/6 for the second term and I just can't work it out, if anyone can help I'd appreciate it. Thanks.