Working out the current flow in a wire

[Bolter]

Homework Statement

Finding the current that flows in the third wire and 20 V battery

Relevant Equations

Ohm's law
Kirchhoff's 1st & 2nd law

Hi there!

I have recently been given this question by my teacher as shown below

I'm struggling to see the set up arrangement for this circuit

This is what I have drawn so far

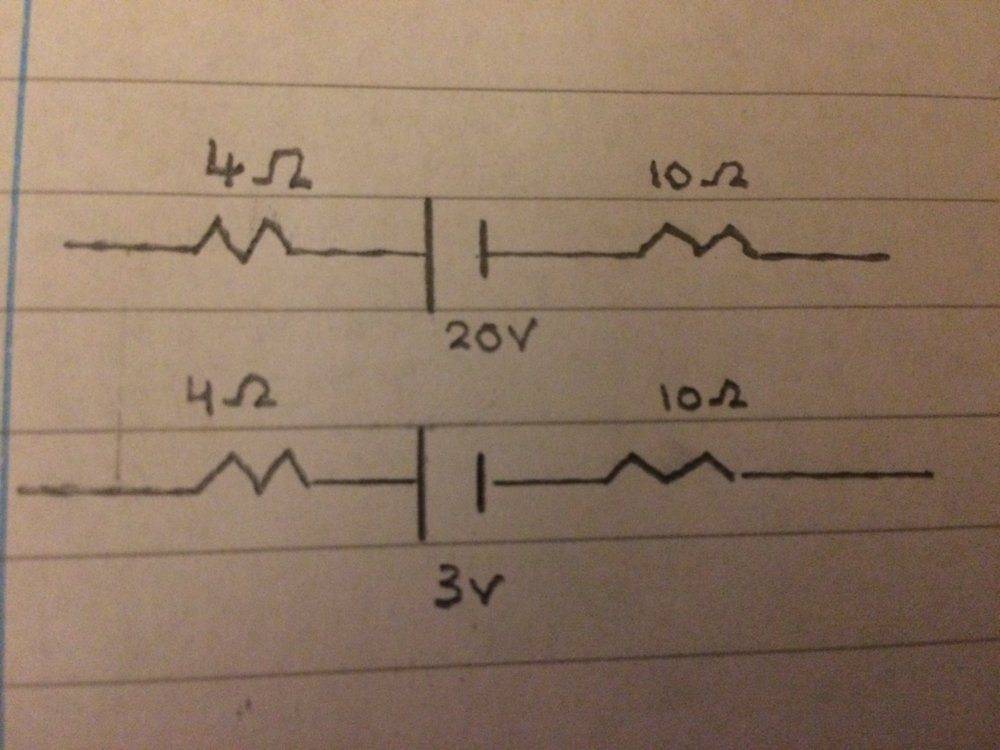
How would I fit in the third wire here and ensure I have closed loop circuit so that current can begin to flow?

Any help would be great! Thanks

 

[etotheipi]

You have included the resistances of the connecting wires twice; first draw the cells with one above the other, and then add on the internal resistances. You are then connecting the poles with wires of $4\Omega$ and $10\Omega$, but you are subsequently also connecting the midpoint of these wires with an $8\Omega$ wire.

If the resistance of the wires increases linearly with length, try splitting the resistances of each of the wires connecting the poles into equal halves. Does this help you to draw the diagram?

 

[Bolter]

You have included the resistances of the connecting wires twice; first draw the cells with one above the other, and then add on the internal resistances. You are then connecting the poles with wires of $4\Omega$ and $10\Omega$, but you are subsequently also connecting the midpoint of these wires with an $8\Omega$ wire.

If the resistance of the wires increases linearly with length, try splitting the resistances of each of the wires connecting the poles into equal halves. Does this help you to draw the diagram?

Thanks I have tried to follow through with what you have said and get my new set up looking like this?

 

[etotheipi]

Thanks I have tried to follow through with what you have said and get my new set up looking like this?

This looks good to me, however to solve the problem you need so separate the $4\Omega$ wire into two $2\Omega$ resistors on either side of the node, and the same goes for the $10\Omega$ wire. If you want justification, it comes from the fact that each of the connecting wires can be thought of as two half wires joined together, and since both have the same length they both have the same resistance.

Then you need to solve for the currents! If you label up the currents in each branch, what equations can you write down from Kirchhoff's two laws?

 

[Bolter]

This looks good to me, however to solve the problem you need so separate the $4\Omega$ wire into two $2\Omega$ resistors on either side of the node, and the same goes for the $10\Omega$ wire. If you want justification, it comes from the fact that each of the connecting wires can be thought of as two half wires joined together, and since both have the same length they both have the same resistance.

Then you need to solve for the currents! If you label up the currents in each branch, what equations can you write down from Kirchhoff's two laws?

Ok so I have tried to construct some equations from Kirchhoff's 2nd law, where I know that sum the voltages around a closed circuit is zero

Do these 2 equations that I have obtained from Kirchhoff's 2nd law look right?

 

[etotheipi]

Ok so I have tried to construct some equations from Kirchhoff's 2nd law, where I know that sum the voltages around a closed circuit is zero

Do these 2 equations that I have obtained from Kirchhoff's 2nd law look right?

They seem fine to me; notice that now you have 3 equations and 3 unknowns:

$I = I_{1} + I_{2}$, $3 = 10I + 8I_{2}$ and $-17 = 10I + 8I_{1}$

This is now just a case of solving the simultaneous equations.

 

[Bolter]

They seem fine to me; notice that now you have 3 equations and 3 unknowns:

$I = I_{1} + I_{2}$, $3 = 10I + 8I_{2}$ and $-17 = 10I + 8I_{1}$

This is now just a case of solving the simultaneous equations.

I have now solved these simultaneously using a bit of substitution and elimination and the results I obtained were

I = –0.5 A
I2 = 1 A
I1 = –1.5 A

This doesn't seem right to me since the answer gives these?

 

[etotheipi]

This doesn't seem right to me since the answer gives these?

The $1.0\text{A}$ and $1.5\text{A}$ currents are the same as you determined for parts a) and b). Perhaps you are concerned about the negative signs of the currents? This just means that your original guess of the direction of the currents happened to be incorrect (this is fine, Kirchhoff's laws are self correcting!), and the currents should in fact be in the opposite direction.

Note also that a faster way to solve the system would be to add the two equations $3 = 10I + 8I_{2}$ and $-17 = 10I + 8I_{1}$. Then you can turn $8I_{1} + 8I_{2}$ into $8I$!

 

[Bolter]

The $1.0\text{A}$ and $1.5\text{A}$ currents are the same as you determined for parts a) and b). Perhaps you are concerned about the negative signs of the currents? This just means that your original guess of the direction of the currents happened to be incorrect (this is fine, Kirchhoff's laws are self correcting!), and the currents should in fact be in the opposite direction.

Note also that a faster way to solve the system would be to add the two equations $3 = 10I + 8I_{2}$ and $-17 = 10I + 8I_{1}$. Then you can turn $8I_{1} + 8I_{2}$ into $8I$!

Ah so these negative signs just indicate that the current is actually flowing in the opposite direction as opposed to the direction that I chose. I see how these current directions fix themselves if I stay consistent throughout with the direction that I initially chose first

Thanks this was quite useful to take in note of!