- #1
Kior
- 11
- 0
Member warned about posting without the template and with no effort
I am preparing for my math probability class next semester. There is question: Calculate E(x3µσ) Would anyone explain the solution in the picture a little bit to me?
1.Why is the step hold? Is there a formula or something that i can calculate E[X-µ]n?
2.Why is the fourth step hold? Where is the σ from and why variance σ2= E[X-µ]2?
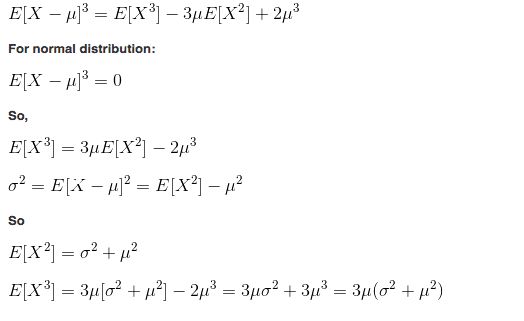
1.Why is the step hold? Is there a formula or something that i can calculate E[X-µ]n?
2.Why is the fourth step hold? Where is the σ from and why variance σ2= E[X-µ]2?