MHB Zero's question at Yahoo Answers regarding polynomial fitting

[MarkFL]

Here is the question:

Write a function for the polynomial that fits the following description.?

write a function for the polynomial that fits the following description.

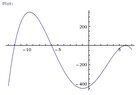
p is a fourth-degree polynomial with x-intercepts -12, -6, and 6 and y-intercept -432;
p(x) is positive only on the interval (-12 , -6 ).

Here is a link to the question:

Write a function for the polynomial that fits the following description.? - Yahoo! Answers

I have posted a link there to this topic so the OP can find my response.

 

[MarkFL]

Hello Zero,

From the given information, we know the polynomial must have a graph resembling the following:

View attachment 629

Since the function does not pass through the $x$-axis at $x=6$, and it is a quartic, meaning it can have at most 4 roots, we know this root is of multiplicity 2.

Now, in order to have a negative $y$-intercept, we know it must have the form:

$f(x)=-k(x+12)(x+6)(x-6)^2$ where $0<k$

To determine $k$, we may use the information regarding its $y$ intercept as follows:

$f(0)=-k(0+12)(0+6)(0-6)^2=-432$

$-12\cdot6^3k=-432=-2\cdot6^3$

$\displaystyle k=\frac{1}{6}$

Hence:

$\displaystyle f(x)=-\frac{1}{6}(x+12)(x+6)(x-6)^2$

Since we are asked for a polynomial, we should expand it fully to find:

$\displaystyle f(x)=-\frac{1}{6}(x+12)(x-6)(x+6)(x-6)=$

$\displaystyle -\frac{1}{6}(x^2+6x-72)(x^2-36)=$

$\displaystyle -\frac{1}{6}(x^4-36x^2+6x^3-216x-72x^2+2592)=$

$\displaystyle -\frac{1}{6}(x^4+6x^3-108x^2-216x+2592)=$

$\displaystyle -\frac{1}{6}x^4-x^3+18x^2+36x-432$

 

[jakncoke1]

Hello Zero,

From the given information, we know the polynomial must have a graph resembling the following:

View attachment 629

Since the function does not pass through the $x$-axis at $x=6$, and it is a quartic, meaning it can have at most 4 roots, we know this root is of multiplicity 2.

Now, in order to have a negative $y$-intercept, we know it must have the form:

$f(x)=-k(x+12)(x+6)(x-6)^2$ where $0<k$

To determine $k$, we may use the information regarding its $y$ intercept as follows:

$f(0)=-k(0+12)(0+6)(0-6)^2=-432$

$-12\cdot6^3k=-432=-2\cdot6^3$

$\displaystyle k=\frac{1}{6}$

Hence:

$\displaystyle f(x)=-\frac{1}{6}(x+12)(x+6)(x-6)^2$

Since we are asked for a polynomial, we should expand it fully to find:

$\displaystyle f(x)=-\frac{1}{6}(x+12)(x-6)(x+6)(x-6)=$

$\displaystyle -\frac{1}{6}(x^2+6x-72)(x^2-36)=$

$\displaystyle -\frac{1}{6}(x^4-36x^2+6x^3-216x-72x^2+2592)=$

$\displaystyle -\frac{1}{6}(x^4+6x^3-108x^2-216x+2592)=$

$\displaystyle -\frac{1}{6}x^4-x^3+18x^2+36x-432$

I really dig your ability to present solutions in a clear and concise manner