frangieh
- 4
- 0
Homework Statement
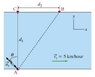
A swimmer wants to cross a river, from point A to point B, as shown in the figure. The distance d_1 (from A to C) is 200 m, the distance d_2 (from C to B) is 150 m and the speed v_r of the current in the river is 5 {km/hour}. Suppose that the swimmer's velocity relative to the water makes an angle of \theta = 45\;{degrees} with the line from A to C, as indicated in the figure.
To swim directly from A to B, what speed u_s, relative to the water, should the swimmer have?