Physics Tutorials

Here contain all the expert written technical physics tutorials for all physics areas. These are technical how-to articles that focus on teaching you a specific skill or how to solve a specific problem. From classic mechanics to general relativity. Self study and classroom strategy. Learn something new today step by step!

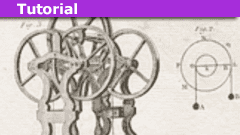
Multi-Atwood Machine Assembly

How to Solve a Multi-Atwood Machine Assembly

/
2 Comments
IntroductionThe figure on the right shows a "double-double" Atwood machine with three ideal pulleys and four masses.  All pulleys are released from…
Variable Mass Systems

How to Apply Newton’s Second Law to Variable Mass Systems

/
0 Comments
Introduction The applicability of Newton's second law in the oft-quoted "general form"  $$\begin{align}\frac{d\mathbf{P}}{dt}=\mathbf{F}_{\text{ext}}\end{align}$$…
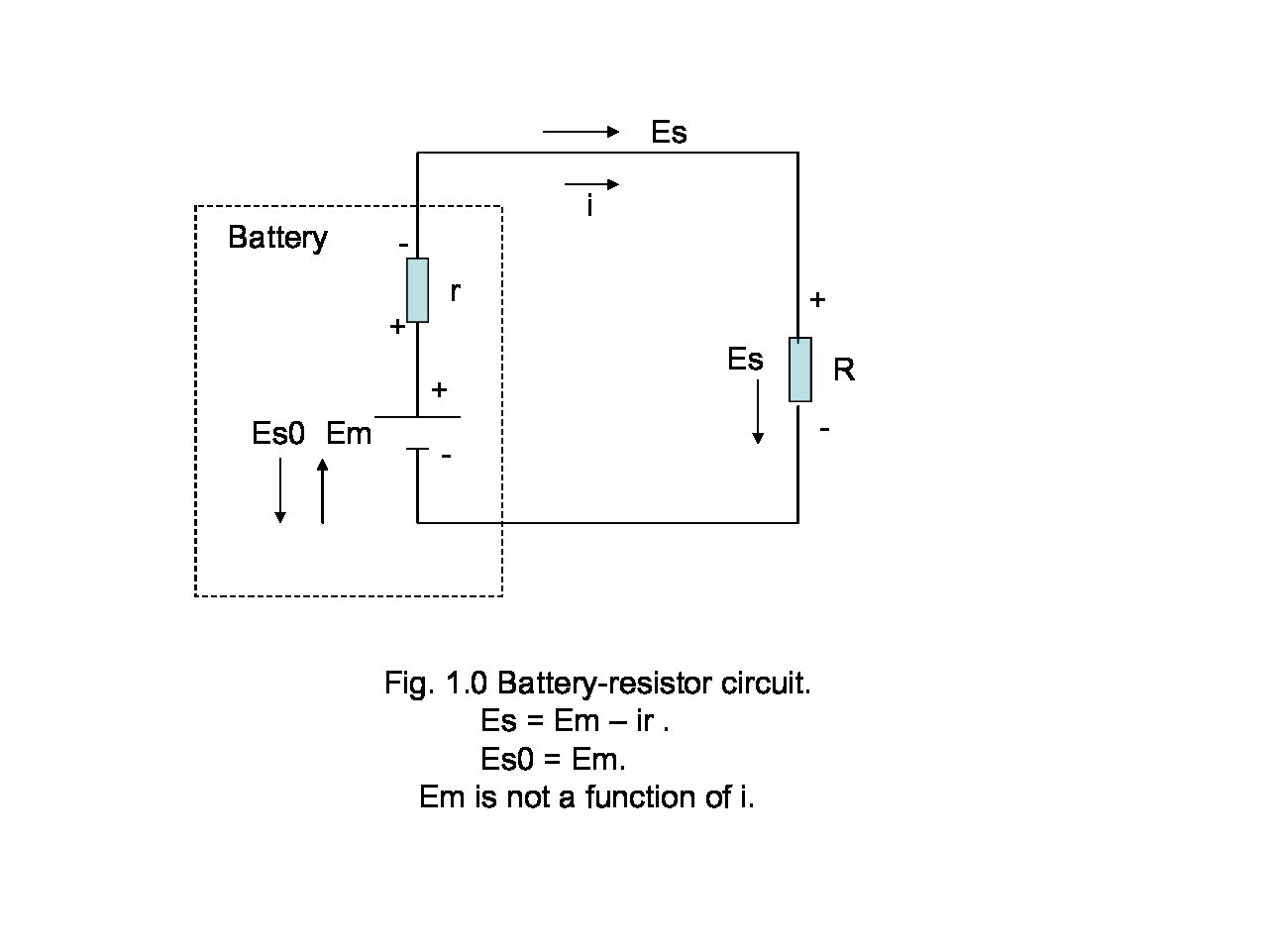
Measure Internal Resistance of Battery

How to Measure Internal Resistance of a Battery

/
0 Comments
Introduction A commonly encountered school-level Physics practical is the determination of the internal resistance of a battery - typically an AA or D…
object slide down ramp physics

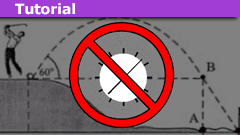
Subtleties Overlooked in Friction Questions: Object Slides Down Ramp

/
0 Comments
Problem statement (simplified) An object slides down a ramp at angle θ to encounter level ground. Both surfaces have kinetic friction: μ' on the ramp,…
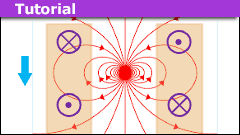
model magnet

How to Model a Magnet Falling Through a Conducting Pipe

/
7 Comments
Introduction In an earlier article, we examined a magnet falling through a solenoid. We argued that the point dipole model can account for the basic features…
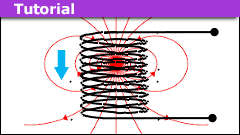
model magnet

How to Model a Magnet Falling Through a Solenoid

/
11 Comments
Introduction Modeling a magnet realistically is a task best done numerically.  Even the simplified model of two separated disks with uniform surface…
Kerr Spacetime

Geodesic Congruences in FRW, Schwarzschild and Kerr Spacetimes

/
5 Comments
Introduction The theory of geodesic congruences is extensively covered in many textbooks (see References); what follows in the introduction is a brief…
MIT course corrections

Corrections to MIT Open Courseware: Systems of Varying Mass

/
1 Comment
Corrections to MIT Open Courseware 8-01sc classical mechanics, fall 2016 Applying Newton's Laws to systems of Varying Mass PDF Course Link My concerns…
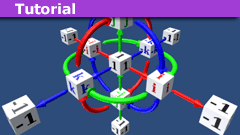
Quaternions in Projectile Motion

Quaternions in Projectile Motion

/
2 Comments
Introduction In a previous Physics Forums article entitled “How to Master Projectile Motion Without Quadratics”, PF user @kuruman brought to our…
solving projectile motion

How to Solve Projectile Motion Problems in One or Two Lines

/
1 Comment
Introduction We show how one can solve most if not all, introductory-level projectile motion problems in one or maybe two lines. To this end, we forgo…
physics cannonball projectile

Maximizing Horizontal Range of a Projectile

/
7 Comments
Introduction A recent homework problem that appeared in the forums was concerned with maximizing the horizontal range of a projectile subject to the launch…
electromagnetic computations duality

A Numerical Electromagnetic Solver Using Duality

/
0 Comments
In the previous insights article (How to Use Duality in Computational Electromagnetic Problems), I covered some uniqueness theorems for the Riemann-Silberstein…
Electric Field Seen by an Observer

The Electric Field Seen by an Observer: A Relativistic Calculation with Tensors

/
0 Comments
This Insight was inspired by the discussion in "electric field seen by an observer in motion", which tries to understand the relation between two expressions:…
valentines reflections graphs

Valentine’s Reflections: Mathematical Matters of the Heart

/
4 Comments
Introduction Being a somewhat geeky Maths 'nerd', I spent days leading up to Valentine's Day trying to find a Maths function appropriate to the day. In…
electromagnetic computations

How to Use Duality in Computational Electromagnetic Problems

/
1 Comment
Some weeks ago I happened across a post that caught my eye. Dale asked a question about the number of photons in an electromagnetic field. His question…
equations of motion

Equations of Motion Revisited

/
1 Comment
Introduction In any school Physics course, the Newtonian equations of motion are very much a 'stock' item. Students learn the equations and are given…
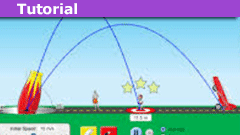
projectile motion

How to Master Projectile Motion Without Quadratics

/
6 Comments
Introduction In a homework thread a while back a PF member expressed dismay along the lines of "Oh no, not another boring projectile motion problem."…
strings waves

Intro to Physically Reasonable Waves on a String

/
4 Comments
Introduction Physics teachers who are either writing physics questions that deal with waves on a string or setting up equipment for a class lab or demo…
elastic ball collision

An Alternate Approach to Solving 2-Dimensional Elastic Collisions

/
4 Comments
Introduction This article follows on from the previous on an alternate approach to solving collision problems. In that article, we determined the equal…

How to Recognize Split Electric Fields

/
1 Comment
Introduction In a previous Insight, A New Interpretation of Dr. Walter Lewin’s Paradox, I introduced the fact that there are two kinds of E fields. …
Mass Generation

An Introduction to the Generation of Mass from Energy

/
28 Comments
Introduction This article is essentially an addition to the previous one on (mainly) inelastic collisions to include the particular case of inelastic…
Collision problems

An Alternative Approach to Solving Collision Problems

/
4 Comments
Introduction Collisions are very much a stock item in any school physics curriculum and students are generally taught about the use of the principles…
maxwell magneto

Maxwell’s Equations in Magnetostatics and Solving with the Curl Operator

/
0 Comments
Introduction: Maxwell's equation in differential form ## \nabla \times \vec{B}=\mu_o \vec{J}_{total}+\mu_o \epsilon_o \dot{\vec{E}}  ##  with ## \dot{\vec{E}}=0…
Learn Dimensional Analysis

Learn the Basics of Dimensional Analysis

/
6 Comments
As a university teacher and as a PF member, I have often noted that students are largely unaware of or not using dimensional analysis to help them in their…
Quantum Mechanical Commutator

The Classical Limit of Quantum Mechanical Commutator

/
8 Comments
The Classical Limit of Commutator (without fancy mathematics) Quantum mechanics occupies a very unusual place among physical theories: It contains classical…
Minkowski Spacetime

Understanding Precession in Special and General Relativity

/
16 Comments
The Absolute Derivative In relativity we typically deal with two types of quantities: fields, which are defined everywhere, and particle properties, which…
isotropy definition

A Formal Definition of Large-Scale Isotropy

/
4 Comments
This Insight is part of my attempt to develop a formal definition of 'large-scale isotropy', a concept that is fundamental to most cosmology, but that…
Kerr Spacetime

Exploring Fermi-Walker Transport in Kerr Spacetime

/
2 Comments
In the last two posts in this series, we developed some tools for looking at Fermi-Walker transport in Minkowski spacetime and then applied them in Schwarzschild…
Minkowski_Spacetime_2

Learning Fermi-Walker Transport in Schwarzschild Spacetime

/
1 Comment
In the first post in this series, we introduced the concepts of frame field, Fermi-Walker transport, and the "Fermi derivative" of a frame field, and developed…
Minkowski Spacetime

Fermi-Walker Transport in Minkowski Spacetime

/
8 Comments
This is the first of several posts that will develop some mathematical machinery for studying Fermi-Walker transport. In this first post, we focus on Minkowski…
rotational mechanics

An Example of Servo-Constraints in Mechanics

/
4 Comments
Servo-constraint was invented by Henri Beghin in his Ph.D. thesis in 1922. For details see the celebrated monograph in rational mechanics by Paul Appell.To…
unity orbital mechanics

Orbital Mechanics in Unity Game Engine for Augmented Reality

/
2 Comments
In this Insight, I’ll go over implementing basic orbital mechanics simulations in the Unity game engine as well as an approach to scaling the simulation…
walter lewin

A New Interpretation of Dr. Walter Lewin’s Paradox

/
65 Comments
Much has lately been said regarding this paradox which first appeared in one of W. Lewin's MIT lecture series on ##{YouTube}^{(1)}##.  This lecture was…
Sagittarius A

How to Calculate the Spin of Black Hole Sagittarius A*

/
3 Comments
This Insight takes a look at how it is possible to calculate the spin of Sagittarius A*, the supermassive black hole at the center of the Milky Way using…
maxima

How to Solve Einstein’s Field Equations in Maxima

/
4 Comments
A few months ago, pervect pointed me to a post by Chris Hillman which is an introduction to the usage of Maxima for General Relativity. Maxima is a free…
ridler_motion2

Rindler Motion in Special Relativity: Rindler Coordinates

/
27 Comments
Our destination In our last article, Hyperbolic Trajectories, we derived some facts about the trajectory of a rocket that is undergoing constant (proper)…
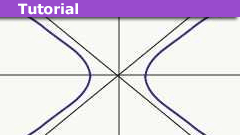
ridler_motion

Rindler Motion in Special Relativity: Hyperbolic Trajectories

/
5 Comments
Introduction: Why Rindler Motion? When students learn relativity, it's usually taught using inertial (constant velocity) motion. There are lots of reasons…
statmech1

Learn Statistical Mechanics: Equilibrium Systems

/
20 Comments
This is the first of a multi-part series of articles intended to give a concise overview of statistical mechanics and some of its applications. These articles…
Parsevalstheorem

Learn an Integral Result from Parseval’s Theorem

/
5 Comments
Introduction: In this Insight article,  Parseval's theorem will be applied to a sinusoidal signal that lasts a finite period of time.  It will be shown…
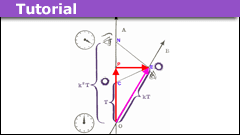
BondiKcalculus

Learn Relativity Using the Bondi K-calculus

/
20 Comments
Although Special Relativity was formulated by Einstein (1905), and given a spacetime interpretation by Minkowski (1908) [which helped make special relativity…
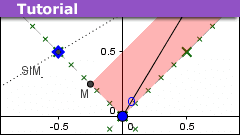
RelativityVariables

Relativity Variables: Velocity, Doppler-Bondi k, and Rapidity

/
8 Comments
Traditional presentations of special relativity place emphasis on "velocity", which of course has an important physical interpretation... carried over…
linearacceleration

Frames of Reference: Linear Acceleration View

/
2 Comments
My previous Insight, Frames of Reference: A Skateboarder's View, explored mechanical energy conservation as seen from an inertial frame moving relative…
inferometer

Fabry-Perot and Michelson Interferometry: A Fundamental Approach

/
14 Comments
Fabry-Perot Effect: The Fabry-Perot effect is usually treated in most optics textbooks as the interference that results from multiple reflections of the…
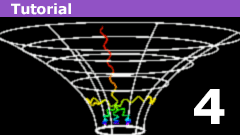
SchwarzschildGeometry4

The Schwarzschild Geometry: Physically Reasonable?

/
33 Comments
 In the last article, we looked at various counterintuitive features of the Schwarzschild spacetime geometry, as illustrated in the Kruskal-Szekeres…
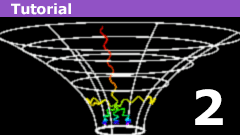
SchwarzschildGeometry2

The Schwarzschild Geometry: Coordinates

/
2 Comments
 At the end of part 1, we looked at the form the metric of the Schwarzschild geometry takes in Gullstrand-Painleve coordinates:$$ ds^2…
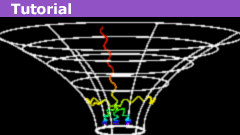
SchwarzschildGeometry1

The Schwarzschild Geometry: Key Properties

/
22 Comments
 Not long after Einstein published his Field Equation, the first exact solution was found by Karl Schwarzschild. This solution is one of the…
rollingmotion

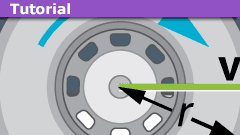
Learn The Basics of Rolling Motion

/
50 Comments
Although rolling wheels are everywhere, when most people are asked "what is the axis of rotation of a wheel that rolls without slipping?", they will answer…
entropy

How to Determine the Change in Entropy

/
9 Comments
How do you determine the change in entropy for a closed system that is subjected to an irreversible process?Here are some typical questions we get…
Schwarzschild

Learn Orbital Precession in the Schwarzschild and Kerr Metrics

/
7 Comments
The Schwarzschild Metric A Lagrangian that can be used to describe geodesics is [itex]F = g_{\mu\nu}v^\mu v^\mu[/itex], where [itex]v^\mu = dx^\mu/ds[/itex]…
spacetimetetrad

Learn About Tetrad Fields and Spacetime

/
1 Comment
A spacetime is often described in terms of a tetrad field, that is, by giving a set of basis vectors at each point. Let the vectors of the tetrad be denoted…

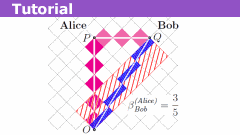
Learn About Relativity on Rotated Graph Paper

/
15 Comments
This Insight is a follow-up to my earlier tutorial Insight (Spacetime Diagrams of Light Clocks). I gave it a different name because I am placing more…
basickinematics

Learn Basic Kinematics in Classical Mechanics

/
8 Comments
There is an interesting thing in teaching of Classical Mechanics. Several theorems which presented below form a core part of kinematics for all Russian…
kinematics

Presenting a Rare Kinematic Formula

/
1 Comment
Here we present some useful kinematic fact which is uncommon for textbooks in mechanics. Consider a convex rigid body (RB) rolling without slipping…
angularvelocity

Elementary Construction of the Angular Velocity

/
1 Comment
Physics books seldom contain an accurate definitions of the angular velocity of a rigid body. I believe that the following construction is as simple as…
physics_vectors

Frequently Made Errors in Vectors – Elementary Use

/
2 Comments
 A vector has magnitude and direction. Pictorially, a vector can be imagined as a location in n-dimensional space relative to some fixed origin. …
lightcone7_3

LightCone 8 Tutorial Part III – How Things are Computed

/
1 Comment
In Part I and Part II of this mini-series, we have briefly discussed the basic user interface and the use of charts to depict the LCDM cosmological model.…
lightcone72

LightCone8 Tutorial Part II – Charts

/
3 Comments
Part I dealt with the basic user interface of LightCone8. This part of the tutorial is about potentially useful cosmological insights to be gained from…
lightcone7

LightCone8 Tutorial Part I

/
2 Comments
LightCone 8 is a versatile tabulating/charting cosmological calculator, useful for understanding the expansion history of the universe (and even some future…
blackholesforce

An Equation for the Centrifugal Force Reversal Near A Black Hole

/
15 Comments
My goal in this article is to derive a simple equation for the proper acceleration of an observer traveling on a circular path around a Schwarzschild black…
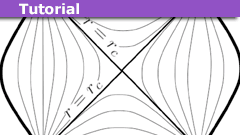
birktheo

Learn A Short Proof of Birkhoff’s Theorem

/
8 Comments
Birkhoff's theorem is a very useful result in General Relativity, and pretty much any textbook has a proof of it. The one I first read was in Misner, Thorne,…
heat errors

Frequently Made Errors in Heat: Elementary Level

/
3 Comments
1. Heat, Work, Internal Energy, and Kinetic Energy "If heat is the motion of molecules, why isn't it Kinetic Energy?"In everyday use, we may think…
Coriolis

Frequently Made Errors: Pseudo and Resultant Forces

/
12 Comments
  1. Real versus Fictitious Pseudo, or "fictitious", forces can arise when a non-inertial frame of reference is used. Using a non-inertial frame…
renormalization2

Why Renormalisation in Quantum Theory Needs a Cutoff

/
31 Comments
Introduction This is a follow on from my paper explaining renormalization. A question was raised - why exactly do we need a cut-off. There is a deep reason…
errors springs

Frequently Made Errors in Mechanics: Springs

/
3 Comments
  1. Springs in Series "A spring of constant ##k_1## is connected in series with a spring of constant ##k_2##.  What is the spring constant…
impact errors

Frequently Made Errors in Mechanics: Momentum and Impacts

/
1 Comment
  An impact is an impulse (change of momentum) that involves arbitrarily large forces acting very briefly. These result in near-instantaneous…
hydrostatics

Frequently Made Errors in Mechanics: Hydrostatics

/
3 Comments
  1. Archimedes' Principle X "When a body is placed in a liquid, the weight of the body equals the weight of the liquid displaced"That will…
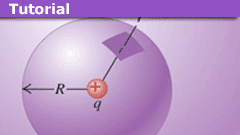
gausslaw

Learn a Partial “Derivation” of Gauss’s Law

/
3 Comments
Gauss's law was formulated by Carl Friedrich Gauss in 1835. It is one of the four Maxwell's equations that form the basis of classical electrodynamics.…
error handling

Frequently Made Errors in Equation Handling

/
15 Comments
  1. Algebra versus Arithmetic When numerical values are provided as inputs in a question, it is tempting to plug these into the equations…
kinematic errors

Frequently Made Errors in Mechanics: Kinematics

/
11 Comments
  Kinematics is the subset of dynamics that only concerns itself with time, displacement, velocity, and acceleration. A problem is…
mistakes moments

Frequently Made Errors in Mechanics: Moments

/
7 Comments
 The term "moment" is used in various ways in Physics and Mathematics:Given a force and a reference point, the force has a moment (or…
renormalization

Quantum Renormalisation Made Easy

/
24 Comments
What Is The Issue With Renormalisation If you have an interest in physics you have likely come across renormalisation before, although what it really…
electrical wire

Misconceiving Mutual Inductance Coefficients

/
4 Comments
 A commonly used formula for mutual inductance M between two nearby coils L1 and L2 is M = k√(L1*L2). This formula however assumes equal percentage…
friction

Frequently Made Errors in Mechanics: Friction

/
8 Comments
  1. Direction of the normal Definition: The normal force that body A exerts on body B is that force of minimum magnitude which suffices to…
forces mistakes

Frequently Made Errors in Mechanics: Forces

/
35 Comments
 Notation: On this page, a circumflex signifies an average. 1. Forces as vectors A force is a vector, i.e. has magnitude and direction.…
2D Animation

How to Visualize the 2-D Particle in a Box

/
11 Comments
Introduction The particle in a box is a staple of entry-level Quantum Mechanics classes because it provides a meaningful contrast between classical and…
Thermodynamics

Understanding Entropy and the 2nd Law of Thermodynamics

/
74 Comments
Introduction The second law of thermodynamics and the associated concept of entropy have been sources of confusion for thermodynamics students for centuries.…