Math Tutorials

Here contains all the math tutorials for all mathematics diciplines. These are technical how-to articles that focus on teaching you a specific skill or how to solve a specific problem. From basic algebra to advanced calculus and beyond. Self study and classroom strategy. Learn new math techniques today!

art of integration

The Art of Integration

/
0 Comments
Abstract My school teacher used to say "Everybody can differentiate, but it takes an artist to integrate." The mathematical reason behind this phrase…
recursion

Reduction of Order For Recursions

/
0 Comments
This is not meant as a full introduction to recursion relations but it should suffice for just about any level of the student.Most of us remember recursion…
hypercube integral

A Novel Technique of Calculating Unit Hypercube Integrals

/
1 Comment
Introduction In this insight article, we will build all the machinery necessary to evaluate unit hypercube integrals by a novel technique. We will first…
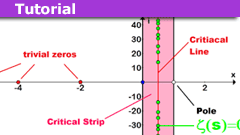
Riemann Hypothesis

The Extended Riemann Hypothesis and Ramanujan’s Sum

/
2 Comments
Riemann Hypothesis and Ramanujan's Sum ExplanationRH: All non-trivial zeros of the Riemannian zeta-function lie on the critical line. ERH: All…
trig special functions

A Trick to Memorizing Trig Special Angle Values Table

/
3 Comments
In calculus classes when you are asked to evaluate a trig function at a specific angle, it's 99.9% of the time at one of the so-called special angles we…
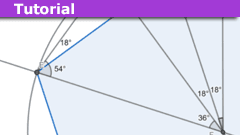
Theorema Primum tutorial

An Introduction to Theorema Primum

/
0 Comments
Introduction Whilst no doubt most frequenters of "Physics Forums" will be familiar with Nicolaus Copernicus as the scientist who advanced the (at the…
python sympy module

Python’s Sympy Module and the Cayley-Hamilton Theorem

/
0 Comments
Two of my favorite areas of study are linear algebra and computer programming. In this article I combine these areas by using Python to confirm that a…
tan rule

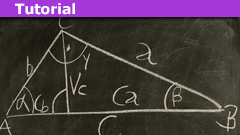
Physical Applications of the “Tan Rule”

/
0 Comments
Introduction Every secondary school student who has encountered trigonometry in his/her Math syllabus will most likely have come across the sine, cosine,…
euler sums

Investigating Some Euler Sums

/
0 Comments
So, why only odd powers? Mostly because the even powers were solved by Leonard Euler in the 18th century. Since the “mathematical toolbox” at that…
Fourier Series Riemann Zeta Function

Computing the Riemann Zeta Function Using Fourier Series

/
5 Comments
Euler's amazing identity The mathematician Leonard Euler developed some surprising mathematical formulas involving the number ##\pi##. The most famous…
impossible triangles

Geometry of Side-side-angle (SSA) and Impossible Triangles

/
0 Comments
What is the ambiguous case? In high school geometry, the idea of proofs is often first introduced to American students. A common task is to use a basic…
calculus

How to Solve Second-Order Partial Derivatives

/
1 Comment
Introduction A frequent concern among students is how to carry out higher order partial derivatives where a change of variables and the chain rule are…
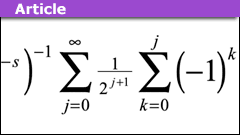
lerch and zeta functions

The Analytic Continuation of the Lerch and the Zeta Functions

/
0 Comments
Introduction In this brief Insight article the analytic continuations of the Lerch Transcendent and Riemann Zeta Functions are achieved via the Euler's…
Integral Representations of Some Special Functions

A Path to Fractional Integral Representations of Some Special Functions

/
9 Comments
Introduction This bit is what new thing you can learn reading this:) As for original content, I only have hope that the method of using the sets $$C_N^n:…
Odd Sums

Explore the Fascinating Sums of Odd Powers of 1/n

/
3 Comments
The goal is to get a little bit closer to the values of the zeta function (ζ(s)) and the eta function (η(s)) for some odd values of s. This insight is…
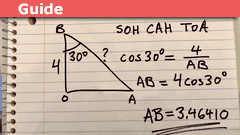
SOHCAHTOA

SOHCAHTOA: Seemingly Simple, Conceivably Complex

/
7 Comments
What is SOHCAHTOA SOHCAHTOA is a mnemonic acronym used in trigonometry to remember the relationships between the sides and angles of right triangles.…
surface integral

Demystifying Parameterization and Surface Integrals

/
3 Comments
Introduction This article will attempt to take the mystery out of setting up surface integrals. It will explain the basic ideas underlying surface integration…

Demystifying the Chain Rule in Calculus

/
7 Comments
Introduction There are a  number of posts on PF involving a general confusion over the multi-variable chain rule.  The problem is often caused by…
unitsworkforyou

How to Make Units of Measurement Work for You

/
13 Comments
How do we use units? You may see one of these speed limit signs, nearly every day. Even though neither of them displays units, drivers know they are implied.…
manifold2

A Journey to The Manifold SU(2): Representations

/
3 Comments
Part 1  Representations Image source: [23]  6. Some useful bases of ##\mathfrak{su}(2,\mathbb{C})## Notations can differ from author…
fourierseries2

Learn Further Sums Found Through Fourier Series

/
5 Comments
In an earlier insight, I looked at the Fourier series for some simple polynomials and what we could deduce from those series. There is a lot more to be…
deriitive5

The Pantheon of Derivatives – Part V

/
2 Comments
  Important Theorems - biased, of course Implicit Function Theorem [1] Jacobi Matrix (Chain Rule). Let ## (x_0,y_0 ) ## be a point in$$U_1…
deriitive4

The Pantheon of Derivatives – Part IV

/
6 Comments
  Lie Derivatives A Lie derivative is in general the differentiation of a tensor field along a vector field. This allows several applications…
deriitive3

The Pantheon of Derivatives – Part III

/
3 Comments
  Some Topology Whereas the terminology of vector fields, trajectories, and flows almost by itself suggests its origins and physical relevance,…
deriitive2

The Pantheon of Derivatives – Part II

/
8 Comments
  Generalizations Beyond ##\mathbb{R}## and ##\mathbb{C}## As mentioned in the section on complex functions (The Pantheon of Derivatives - Part…
deriitive

The Pantheon of Derivatives – 5 Part Series

/
3 Comments
  Differentiation in a Nutshell I want to gather the various concepts in one place, to reveal the similarities between them, as they are often…
integraltrick

Trick to Solving Integrals Involving Tangent and Secant

/
6 Comments
This little trick is used for some integration problems involving trigonometric functions is probably well-known, but I only learned it yesterday. So…
FourierSeries

Using the Fourier Series To Find Some Interesting Sums

/
4 Comments
Preliminaries If f(x) is periodic with period 2p and f’(x) exists and is finite for -π<x<π, then f can be written as a Fourier series: [itex]f(x)=\sum_{n=-\infty}^{\infty}a_{n}e^{inx}…
partial-differentiation

Learn Partial Differentiation Without Tears

/
6 Comments
Differentiation is usually taught quite well. Perhaps that's because it is the first introduction to calculus, which is considered a big step in a student's…
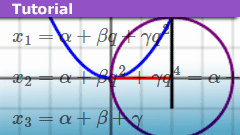
cubicfunction

Learn How to Solve the Cubic Equation for Dummies

/
5 Comments
Everybody learns the "quadratic formula" for solving equations of the form [itex]A x^2 + B x + C = 0[/itex], even though you don't really need such a formula,…
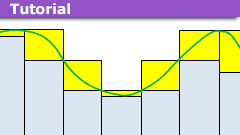
omissionguage

Omissions in Mathematics Education: Gauge Integration

/
31 Comments
The current (pure) mathematics curriculum at the university is well-established. Most of the choices made are sensible. But still, some important topics…
Brachistochrone

Explaining the General Brachistochrone Problem

/
3 Comments
Consider a problem about the curve of fastest descent in the following generalized statement. Suppose that we have a Lagrangian system $$L(x,\dot x)=\frac{1}{2}g_{ij}(x)\dot…
integralmisconceptions

Some Misconceptions on Indefinite Integrals

/
40 Comments
Integration is an incredibly useful technique taught in all calculus classes. Nevertheless, there are certain paradoxes involved with integration that…
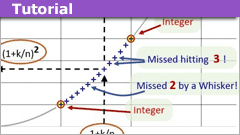
irrationalnumbers

Mathematical Irrationality for Dummies

/
13 Comments
On one of my restless wanderings around the Internet, I came upon a collection of proofs of the statement that the square root of 2 is an irrational…
complexexponents

Learn Complex and Irrational Exponents for the Layman

/
5 Comments
This Insight is part of our "Young Authors" series, where talented young students showcase their knowledge.  This is how both you and I learned…
Eigenvectors

What Are Eigenvectors and Eigenvalues in Math?

/
37 Comments
Two important concepts in Linear Algebra are eigenvectors and eigenvalues for a linear transformation that is represented by a square matrix. Besides…
partialfractions

Introduction to Partial Fractions Decomposition

/
3 Comments
Partial fractions decomposition is an algebraic technique that can be used to decompose (break down) a product of rational expressions into a sum…
ODE2

How to Solve Nonhomogeneous Linear ODEs using Annihilators

/
5 Comments
My previous Insights article, Solving Homogeneous Linear ODEs using Annihilators, discussed several examples of homogeneous differential equations, equations…
ODE1

Solving Homogeneous Linear ODEs using Annihilators

/
8 Comments
In this Insights article we'll look at a limited class of ordinary differential equations -- homogeneous linear ODES with constant coefficients. Although…
lineartransformations

Learn About Matrix Representations of Linear Transformations

/
19 Comments
Let X and Y be finite-dimensional vector spaces. Let ##T:X\to Y## be a linear transformation. Let ##A=(e_1,\dots,e_n)## and ##B=(f_1,\dots,f_m)## be ordered…
cardinalnumbers

Informal Introduction to Cardinal Numbers

/
1 Comment
Cardinal numbers We will now give an informal introduction to cardinal numbers. We will later formalize this by using ordinal numbers. Informally, cardinal…
999

Is There a Rigorous Proof Of 1 = 0.999…?

/
102 Comments
Yes.First, we have not addressed what 0.999... means. So it's best first to describe what on earth the notation [tex]b_0.b_1b_2b_3...[/tex] means.…
Distributions

Errors in Probability: Continuous and Discrete Distributions

/
1 Comment
1. Classifying as discrete, continuous, or mixed These statements (or equivalents) can be found in authoritative-seeming websites:X "A random variable…
natural language errors

Frequently Made Errors in Probability: Conditionals in Natural Language

/
2 Comments
  1. Turning a verbal condition into Algebra An actual thread..."A study of auto accidents has found that 40% of all fatal accidents are…
variables

Some Conceptual Difficulties in the Roles of Variables and Constants

/
3 Comments
1. Variables and Constants When is a constant not a constant?  When it varies.In the standard equation ##y=ax+b##, we are used to thinking of x and…
differentiable function 2

A Continuous, Nowhere Differentiable Function: Part 2

/
2 Comments
This is Part 2 of a series of articles in which the goal is to exhibit a continuous function that is nowhere differentiable and to explore some interesting…
differentiable function

A Continuous, Nowhere Differentiable Function: Part 1

/
12 Comments
When studying calculus, we learn that every differentiable function is continuous, but a continuous function need not be differentiable at every point.…