
The Lambert W Function in Finance
/
0 Comments
Preamble
The classical mathematician practically by instinct views the continuous process as the "real" process, and the discrete process as an approximation…

Why Division by Zero is a Bad Idea
A division by zero is primarily an algebraic question. The reasoning therefore follows the indirect pattern of most algebraic proofs:
What if it was allowed?
Then…
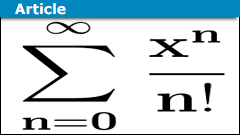
Series in Mathematics: From Zeno to Quantum Theory
Introduction
Series play a decisive role in many branches of mathematics. They accompanied mathematical developments from Zeno of Elea (##5##-th century…

Differential Equation Systems and Nature
Abstract
"Mathematics is the native language of nature." is a phrase that is often used when it comes to explaining why mathematics is all around in natural…

Beginners Guide to Precalculus, Calculus and Infinitesimals
Introduction
I am convinced students learn Calculus far too late. In my view, there has never been a good reason for this.In the US, they go through…

What Are Numbers?
Introduction
When doing mathematics, we usually take for granted what natural numbers, integers, and rationals are. They are pretty intuitive. Going…

Introduction to the World of Algebras
Abstract
Richard Pierce describes the intention of his book [2] about associative algebras as his attempt to prove that there is algebra after Galois…

What Are Infinitesimals – Advanced Version
Introduction
When I learned calculus, the intuitive idea of infinitesimal was used. These are real numbers so small that, for all practical purposes (say…

An Overview of Complex Differentiation and Integration
Abstract
I want to shed some light on complex analysis without getting all the technical details in the way which are necessary for the precise treatments…

When Lie Groups Became Physics
Abstract
We explain by simple examples (one-parameter Lie groups), partly in the original language, and along the historical papers of Sophus Lie, Abraham…
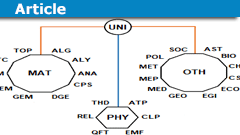
Classification of Mathematics by 42 Branches
I often read questions about our classification scheme that we use on physicsforums.com to sort posts by science fields and subjects, what has…

Counting to p-adic Calculus: All Number Systems That We Have
An entire book could easily be written about the history of numbers from ancient Babylon and India, over Abu Dscha'far Muhammad ibn Musa al-Chwarizmi (##\sim…

Évariste Galois and His Theory
* Oct. 25th, 1811 † May 31st, 1832
... or why squaring the circle is doomed.
Galois died in a duel at the age of twenty. Yet, he gave…
Yardsticks to Metric Tensor Fields
I asked myself why different scientists understand the same thing seemingly differently, especially the concept of a metric tensor. If we ask a topologist,…
P vs. NP and what is a Turing Machine (TM)?
P or NP
This article deals with the complexity of calculations and in particular the meaning of
##P\stackrel{?}{\neq}NP##
Before we explain what P and…
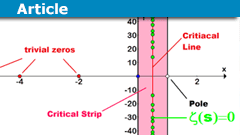
The History and Importance of the Riemann Hypothesis
Riemann Hypothesis History
The Riemann Hypothesis is one of the most famous and long-standing unsolved problems in mathematics, specifically in the field…
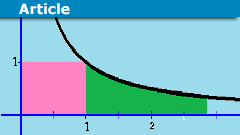
The Amazing Relationship Between Integration And Euler’s Number
We use integration to measure lengths, areas, or volumes. This is a geometrical interpretation, but we want to examine an analytical interpretation that…

Probabilistic Factors Involved in Disease and Virus Testing
Introduction
This Insight looks at the various probabilistic factors and related terminology involved in disease and virus testing.As we all know,…

10 Math Things We All Learnt Wrong At School
The title is admittedly clickbait. Or a joke. Or a provocation. It depends on with whom you speak, or who reads it with which expectation. Well, I cannot…

How Bayesian Inference Works in the Context of Science
Confessions of a moderate Bayesian part 3
Read part 1: How to Get Started with Bayesian Statistics
Read part 2: Frequentist Probability vs Bayesian ProbabilityBayesian…
Exploring Frequentist Probability vs Bayesian Probability
Confessions of a moderate Bayesian, part 2
Read Part 1: Confessions of a moderate Bayesian, part 1Bayesian statistics by and for non-statisticianshttps://www.cafepress.com/physicsforums.13280237
Background
One…
How to Get Started with Bayesian Statistics
Confessions of a moderate Bayesian, part 1
Bayesian statistics by and for non-statisticianshttps://www.cafepress.com/physicsforums.13265286
Background
I…

Mathematician Mary Somerville Features in Google Doodle
The Google Doodle for 2 February 2020 celebrated Mary Somerville, the Scottish polymath and science writer, and with Caroline Herschel, the joint first-ever…
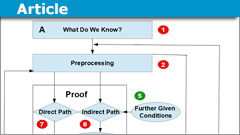
How to Write a Math Proof and Their Structure
Proofs in mathematics are what mathematics is all about. They are subject to entire books, created entire theories like Fermat's last theorem, are hard…
A Pure Hamiltonian Proof of the Maupertuis Principle
Here is another version of proof of Maupertuis's principle. This version is pure Hamiltonian and independent of the Lagrangian approach.The proof…

The Sum of Geometric Series from Probability Theory
Here I present a simple (but to the best of my knowledge, new) derivation of the formula for the sum of the infinite geometric series. The derivation is…

Lie Algebras: A Walkthrough The Representations
Part III: Representations
10. Sums and Products.
Frobenius began in ##1896## to generalize Weber's group characters and soon investigated…

Learn Lie Algebras: A Walkthrough The Structures
Part II: Structures5. Decompositions.Lie algebra theory is to a large extend the classification of the semisimple Lie algebras…

Learn Lie Algebras: A Walkthrough The Basics
Part I: Basics
1. Introduction.
This article is meant to provide a quick reference guide to Lie algebras: the terminology, important theorems,…

Learn a Simplified Synthesis of Financial Options Pricing
Financial options (the right to purchase ("call") or sell ("put") stock (or other assets)) at a fixed price at a future date have been around for a long…
Learn the Basics of Hilbert Spaces and Their Relatives: Operators
Operators. The Maze Of Definitions.
We will use the conventions of part I (Basics), which are ##\mathbb{F}\in \{\mathbb{R},\mathbb{C}\}##,…
Learn the Basics of Hilbert Spaces and Their Relatives
Basics
Language first: There is no such thing as the Hilbert space.Hilbert spaces can look rather different, and which one is used in…

Learn About Intransitive Dice with a Twist
Intransitive dice are sets of dice that don't follow the usual rules for "is better/larger than". If A<B and B<C, then A<C. If Bob runs faster…

A Journey to The Manifold SU(2): Differentiation, Spheres, and Fiber Bundles
Part 2
Differentiation, Spheres, and Fiber Bundles
Image source: [24]The special unitary groups play a significant role in the standard…

How to Tell Operations, Operators, Functionals, and Representations Apart
All these concepts belong to the toolbox of physicists. I read them quite often on our forum and their usage is sometimes a bit confusing.…

When Simple Geometry Unveils Deep Math
Introduction
It is a remarkable fact that consideration of very elementary concepts in geometry often leads quickly into deep and unexpected mathematical…

Linear Representations and Why Precision is Important in Math
First of all: What is a representation? It is the description of a mathematical object like a Lie group or a Lie algebra by its actions on another space…
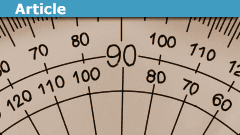
Can Angles be Assigned a Dimension?
1. Some Background on Dimensional Analysis
... if you are not already familiar with it.
1.1 Dimensions
Dimensional Analysis is a way of analyzing…

Exploring the Relationship Between Group Theory and Geometry
There is a very deep link between group theory and geometry. Sadly, this link is not emphasized a lot in most courses of group theory, even though it is…

An Interesting Ramsey Theory Riddle
Ramsey theory has its origins in a very nice riddle
Consider a party of 6 people. Any two of these 6 will either be meeting each other for the first time…

Scientific Inference: Balancing Predictive Success with Falsifiability
Bayes' Theorem: Balancing predictive success with falsifiability
Despite its murky logical pedigree, confirmation is a key part of learning.…

Is It Possible to Design an Unbreakable Cipher?
Is it possible to design an unbreakable cipher?
Do methods of encryption exist that guarantee privacy from even the most capable and highly-resourced…

The Monographic Substitution Cipher: From Julius Caesar to the KGB
A monographic substitution cipher works by replacing individual characters of plaintext with corresponding characters of ciphertext. It is perhaps the…
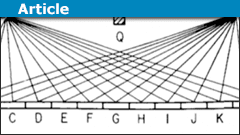
Hear the Case for Learning Complex Math
Resistance to complex math seems to never die out. I see it frequently in PF posts. Often it takes the form of challenges rather than questions. …

Things Which Can Go Wrong with Complex Numbers
At the first sight, there are many paradoxes in complex number theory. Here are some nice examples of things that don't seem to work:Example A
[itex]-1=i^2=\sqrt{-1}\cdot\sqrt{-1}=\sqrt{(-1)(-1)}=\sqrt{1}=1[/itex]Example…

Intro to the Millennium Prize Problems
IntroductionIn this Insight, I will go over the background information for the Millennium Prize problems and briefly describe three of them. A future…
Learn Axioms for the Natural Numbers
** Bloch Chapter 1.2The Peano system in Bloch has a special element ##1\in \mathbb{N}##. The intuitive idea here is that ##\mathbb{N} = \{1,2,3,...\}##.…

An Intro on Real Numbers and Real Analysis
It is important to realize that in standard mathematics, we attempt to characterize everything in terms of sets. This means that notions such as natural…

Trials and Tribulations of a Physicist who Became a Math Geek
How did I go from the brink of changing my major from physics to ceramics (no more math) to the Math faculty of the Air Force Academy? How did I go from…

Lessons From My Experience Teaching Math
My #1 goal, when I teach a math class, is to convey a certain way of thinking about math. It's quite different from what my students have done before,…

A Brachistochrone Subway Is Not a Cost-effective Idea
It is apparent that a subway tunnel could be built without the need for supplied energy like electricity, assuming zero friction everywhere. The tunnel…

Is Zero a Natural Number?
Using: Anderson-Feil Chapter 1.1
Is zero a natural number?
This is a pretty controversial question. Many mathematicians - especially those working in…

What is a Property Formally in Mathematical Logic
** Hrbacek-Jech Chapter 1.2Hrbacek and Jech do not go into full detail about what a property is formally. This is a part of mathematical logic, but…
