yungman
- 5,741
- 294
I am studying Poynting vectors. I run into question that I don't see any good explanation in all the books I have. All the books claimed
E_{(z,t)} =E_{(z=0)} Re[e_{j(wt-\beta z)} + \Gamma e_{j(wt+\beta z)}]
But sinse E0 is complex so this is what I have and is not equal to what the book gives. In fact the Electromagnetic by Ulaby actually say ignor the phase angle of E0! Below is what I have:
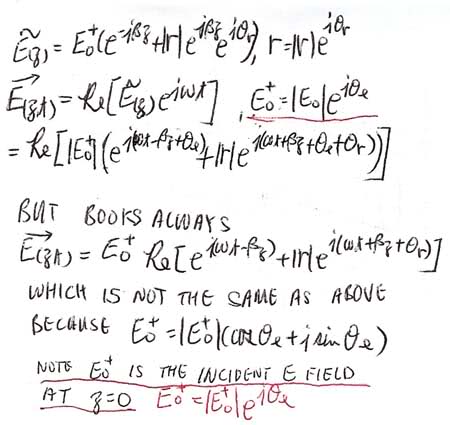
Obviously the answer does not agree. This is particularly obvious when working on Poynting vectors. Please tell me what do I miss in this whole thing.
Thanks
E_{(z,t)} =E_{(z=0)} Re[e_{j(wt-\beta z)} + \Gamma e_{j(wt+\beta z)}]
But sinse E0 is complex so this is what I have and is not equal to what the book gives. In fact the Electromagnetic by Ulaby actually say ignor the phase angle of E0! Below is what I have:
Obviously the answer does not agree. This is particularly obvious when working on Poynting vectors. Please tell me what do I miss in this whole thing.
Thanks
Last edited: