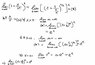On why e^x = lim (1+x/n)^n

AxiomOfChoice

Is there someone who can explain why this is true, or point me to an online resource that provides a proof of it?
[tex]
e^x = \lim_{n\to \infty} \left(1 + x/n \right) ^n
[/tex]
I know that in some ways, this is how the exponential function is defined. But any resources you can provide that explain it in more detail would be appreciated. Thanks!

mathman

I am not sure if this will satisfy you.
However expand (1+x/n)ⁿ by the binomial theorem. Take the term by term limit as n -> oo. The result is the power series for e^x.

lurflurf

The reason is when n is large we have
1+x/n~exp(x/n)
we also have (n need not be large)
exp(x/n)^n=exp(x)

The proof depends on ones definition of e^x such as
1)exp'(x)=exp(x) with exp(0)=1
2)exp(x)exp(y)=exp(x+y) with exp'(0)=1
3)exp(x)=1+x+x^2/2!+...+x^n/n!+...
4)exp(log(x))=x log having been previously defined

A common one given 3) is to expand (1+x/n)^n by the binomial theorem and then shown the limit of the sum is the sum of the limits.

Bohrok

Let f(x) be the right side, then rewrite it as e^lnf(x). With ln(f(x)), rearrange it so you can use l'Hôpital's rule (with respect to n), probably use a substitution, and then you can evaluate the limit.

lurflurf

Why does everybody like l'Hôpital's rule so much? It is not needed here as log'(1)=1 suffices.

elibj123

I wrote the proof for you

Attached Thumbnails

 

l'Hôpital

Are you kidding? l'Hôpital's rule is the best. Made of epic win.

As for the OP, yeah, generally, if you let the limit be a variably, say y, you could ln both sides, and solve it that way.

neelakash

Might be I am little late with this post...however,let me say that I could not understand how L Hospital's would have to be implemented to do this...I could follow the binomial expansion argument or the use of standard limit argument.

A second issue...From the texts that deal with symmetry,the limit is also used with operator argument.Like

[tex]\displaystyle\lim_{k\to\infty}\ [\ I_{\ n\times\ n}\ + \frac{\ i \vec{\phi}\ . \mathbb{D} }{k}]^\ {k}[/tex]

[tex] = \ exp\{ \ {\ i \ {\vec{\phi}\ . \mathbb{D} } \}[/tex]

neelakash

I am sorry that it took time to fix the Latex symbols...Let me get back to the discussion...For operator valued argument,the identity also holds...My question is will the relation still hold if [tex]\mathbb{D}=\mathbb{D}_{1}\ +\mathbb{D}_{2}[/tex] and the two operators D1 and D2 do not commute...?

I think it will(as for angular momentum matrices,which are generators of rotation),but how to see it?

l'Hôpital

[itex]
y = \lim_{n\to \infty} \left(1 + x/n \right) ^n
[/itex]

Right? So
[itex]
ln y = ln [ \lim_{n\to \infty} \left(1 + x/n \right) ^n]
[/itex]

Focus on the right, it looks kinda like this ...

[itex]
\lim_{n\to \infty} \left n ln [(1 + x/n \right)]
[/itex]

The n goes to the front because of logarithms.

[itex]
\lim_{n\to \infty} \left (1/n)^-1 ln [(1 + x/n \right)]
[/itex]

If you take the limit, you get [itex]0/0[/itex] So, apply l'Hôpital's rule and you'll get

[itex]
ln y = \lim_{n\to \infty} \left x/(1+x/n) = x [/itex]

So, cancel the ln, and you get as desired,

[itex]

y = e^x [/itex]

neelakash

But can you write in general

[itex]

ln [ \lim_{n\to \infty} \left(1 + x/n \right) ^n]=\ lim_{n\to \infty} \left n ln [(1 + x/n \right)]

[/itex]

I vaguely remember,from outside, one can insert ln inside [lim n-->0] with some condition satisfied...I cannot remember what the condition was...

l'Hôpital

The condition is about continuity. ln is continuous, so yeah, you can move the limit inside or outside.

neelakash

thanks...I forgit it...

mrm0607

Hi,

I would like to understand

how l'Hôpital's rule applies. we haven't covered it yet.

Thank you

mrm0607

Hi,

We have not covered the l Hopitals rule yet so I am trying to expand (1+x/n)^n to show

as lim(n-->infinity) (1+x/n)^n = e^x for any x> 0

This is what I did so far and after that I am short of lost:

Please read this (n 1) in vertical form ( I do not know how to use Latex)

lim (n-->infinity)(1 + x/n)^n =

lim(x->infinity)[1 + (n 1) (1/n) + (n 2)(1/n^2) + (n 3)(1/n^3) ---------- + --
-- (n k)(1/n^k) + ---+(n n)(1/n^n)]

=1 + 1/1! + 1/2! + 1/3! + ---- 1/k! + --- + 1/n!

now how does this lead to e^x?

May be I did not understand what you meant?

Thank you.