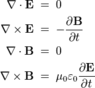Maxwell's equations VS. Lorentz & Coulomb force equations

varga

I find Maxwell's equations insufficient and superfluous having the Lorentz & Coulomb's force equations. As far as I see magnetic (Lorentz force) and electric (Coulomb's force) interaction is best defined by these two equations themselves, and although Maxwell's equations can describe quite a few electromagnetic interactions, by not having Lorentz force incorporated in any equation nor included as separate one, Maxwell's equations are automatically doomed to fail to describe any interaction due to this very, very important force. Did I miss something?

Why describe electric interaction with any other but with 'Electric force' equation?

Why describe magnetic interaction with any other but with 'Magnetic force' equation?


*** Electric interaction
Step 1: Electric field potential given by Coulomb's law
Step 2: Electric force (acceleration vector) given by Coulomb's law

*** Magnetic interaction
Step 3: Magnetic field potential given by Biot-Savart law
Step 4: Magnetic force (acceleration vector) given by Lorentz force
====================================================

As far as I see that's all what is necessary to solve any em interaction, no?



1. Gauss's law
- This is obviously about Coulomb's law/electric potential, so why would this equation be "more suitable"?


2. Gauss's law for magnetism
- divB = 0, what in the world? Instead of to describe magnetic potentials or force, to put here Biot-Savart law, or Lorentz force equation or Ampere's force law, they included some equation that has result already calculated in advance? No monopoles? That's as useful as stating "there is no other intelligent life in the Universe".


3. Faraday's law of induction
- Is there anything here we can not calculate with the time integral of four steps given above? How is this induction supposed to accurately describe complete interaction if it is oblivious to Lorentz force?


4. Ampère's circuital law
- Is there anything here we can not calculate with the time integral of four steps given above? This is the best candidate to be saying something about Lorentz force, if it only included "Ampere's force law" too.



I suppose the explanation why these equations are in this form is because that is the most suitable for practical application and experimental setups, but still, my greatest concern is how any of that can accurately work without incorporating Lorentz force and Biot-Savart law in the same fashion as Coulomb's law and electric potential/force.

DaleSpam

You do need all four of Maxwell's equations and the Lorentz equation. Biot-Savart is only an approximation to Maxwell.

Born2bwire

To reiterate, practically the entirety of all classical electrodynamics is derived from Maxwell's equations and the Lorentz force. You really do not need much more than that. Practically any set of equations that you can reference are derivable from these five equations (Coulomb's Law (only valid for electrostatics), Biot-Savart (only valid for magnetostatics), Lorentz transformations (special relativity is automatically satisfied in Maxwell's equations), etc.). Still, Lorentz force is only really needed in terms of trajectory problems. Maxwell's equations already incorporate charge and current sources. Thus we do not need to go through the Lorentz force as a mediator for inducing current sources from fields for many problems.

kcdodd

You can think of maxwells equations as equations of motion for the field, and the lorentz force as EOM for the currents. If you are looking for a single equation, it is the EM lagrangian, which will get you to all the equations of motion for the field and currents.

espen180

Electromagnetic waves? Ampere's Law and Faraday's Law together give the velocity and E/B ratio in electromagnetic waves. There are no charges or magnetic dipoles present in the wave. The electric and magnetic field sustain eachother. Can you explain that using your time integral 4-step method?

The knowledge that radiowaves, infrared, visible light, x-rays and gamma rays all are the same phenomenon but with different energies, the prediction of the speed of light and probably the theory of relativity are thanks to Maxwell's equations.

SpectraCat

How are you gonna get them accelerated electrons to emit EM radiation using your 4 step program above? Maxwell's equations and the Lorentz equation accurately describe *all* classical physical phenomena involving electricity and magnetism .. any proposed "substitute" would also need to do that, at the very least.

varga

I'm glad you mentioned it. What waves? Yeah, I know how text-book description goes, but none of these equations has to do anything with any radiation, these equations are used to describe experimental setups with current carrying wires and permanent magnets, where properties are measured in amperes, volts, ohms and millimeters. How any of this has anything to do with any em WAVES? It is about fields, not waves. But if Maxwell's equations can describe photons, then Lorentz and Coulomb's force equations can too.


Ok, tell me what experiment are you talking about, show the result given by Maxwell's equations and I will demonstrate I can do the same, or better, with the four steps above.

Electric and magnetic fields do not sustain each other. According to Coulomb's law, Lorentz force and Biot-Savart law, electric field is intrinsic property of any single electron (charge), while magnetic fields forms proportionally to velocity, there is no creation of any other fields here, there will always be electric field whose potential magnitude will be independent of everything, and the magnitude potential of the magnetic field of moving charge will vary according to velocity vector.

Magnetic field is EFFECT of charge motion, it is not the CAUSE for it, however since all moving electrons can interact with this magnetic field, what it can do is to cause electron displacement, i.e. it can cause electric CURRENT, but that does not mean it can be the CAUSE or CREATE any new electrostatic potential.


Can you point out what Maxwell's equation predicts the speed of light? And again, what Maxwell's equation says anything about any photons (em radiation)?

varga

You are not talking about synchrotron radiation again, or do you?

I really have no idea how Maxwell's equations do it, what are you referring to?



I agree that together with the Lorentz force they do describe all. What I'm saying is that Lorentz force in this form "F= q(E + v x B)", where it is integrated with Coulomb's force, can do it alone. One equation VS. four, do you accept the challenge?

espen180

Derivation of the speed of light.
Note that it skips a step. Instead of showing the final wave equations using the permeability and permittivity constants the author immediately substitutes them.

Compare with this to see that Maxwell's equations, using constants measures from electrostatics and magnetostatics, really does predict the wave nature and speed of electromagnetic waves.
Wave equation

Note that this was before quantum physics and thus the model was later exanded to account for the particle nature of light.

DaleSpam

The Lorentz force and the Coulomb's force is woefully inadequate:
1) no way to calculate the magnetic field
2) no waves
3) no interaction between magnetic field and electric field
4) infinite speed of a propagating electric field

varga

1) no way to calculate the magnetic field

Step 3.

F= q(E + v x B); E here refers to Coulomb's Law, and B to Biot-Savart law, or at least I'll define it like that, so that basically unrolls to these four:

*** Electric interaction
Step 1: electric field potential given by Coulomb's law
Step 2: Electric force (acceleration vector) given by Coulomb's law

*** Magnetic interaction
Step 3: Magnetic field potential given by Biot-Savart law
Step 4: Magnetic force (acceleration vector) given by Lorentz force
====================================================

- How Maxwell's equations calculate magnetic field?


2) no waves

- I'll make them just like they did. What do you think E and B stand for in Maxwell's equations?


3) no interaction between magnetic field and electric field

- Magnetic and electric fields DO NOT interact.


4) infinite speed of a propagating electric field

- What is propagation speed of E and B fields in Maxwell's equations? What is the expression for E and B?

varga

Thanks, that's very interesting. Do you think you could explain the process or point someplace I can find answer to these questions:

- "To obtain the electromagnetic wave equation in a vacuum using the modern method, we begin with the modern 'Heaviside' form of Maxwell's equations. In a vacuum and charge free space, these equations are:




Taking the curl of the curl equations gives:




- What in the world curl of E and B fields, and even the curl-of-the-curl, is supposed to have with the speed of light? What are they trying to do here, how did anyone ever figure out they should combine curls to get any information about any speed?

- How can we talk about any velocity if we are not calculating FORCES, how can field potentials and their shape tell us anything about any velocity without calculating the FORCE and ACCELERATION first? I need to understand what and WHY they did so I can do the same thing with "my" equations.



Is this it, the beginning of it? As a time integral my equations are already in similar form like this, can you help me make a 'wave equation' out of it?

Matterwave

I'm just going to address this one point. If magnetic and electric fields don't interact, then how can you get propagation of an EM wave? In an electro-magnetic wave, the changing electric fields induce a changing magnetic field and vice-versa. That's how you get to propagate that wave out.

How would you explain all of EM radiation if you assert that electric fields and magnetic fields don't interact? I would like to know this.

Born2bwire

Electromagnetic waves do not need sources to propagate. There are no forces or accelerations, there are no charges or currents.

We are the ones that are telling you that it will not work. Why should we attempt to work out assertions that are unanimously being detracted?

Again, you are using static equations for time-varying situations. This will not work.

DaleSpam

That's fine, you can certainly use Biot-Savart to calculate a B field, but you cannot derive Biot-Savart from Coulomb and Lorentz force, so this is a third equation.

I would very much like to see that. Kindly post your derivation of the wave equation from only Coulomb, Lorentz force, and Biot-Savart.

Yes, they do. Google "induction".

c, which agrees with experiment. Infinity does not.

varga

Photon is made of how many electric and magnetic fields, you say?

Please show me that equation where I can see how E and B interact.

I'm using the same E and B fields as Maxwell, only I do calculations per point particle, so why do you think I would not to arrive to the same result?




- What is the relation between the speed of light and the curl of the curl of E and B field?

- Can E and B interact, do we add magnetic and electric vectors, do we superimpose them, or do electric only interact with electric and magnetic with magnetic fields?


How about we take on some practical experiment and actually see what will work and what will not work?




Me too, but without any help, I'll need time. Do you think Maxwell's equations were not derived from Coulomb's law and Biot-Savart law?


No, they do not. I explained 'induction' above. Please, show the equation you believe describes this interaction of E and B field.


What is expression for E and B in Maxwell's equations?




Yes, kind of like that, but the other way around.
This the whole point behind my arguments, thanks for that.


1.) Maxwell's equation are about em field potentials - Coulomb's law and Biot-Savart law, but approximated in relation to currents and charge densities.

2.) Lorentz force equation is about em fields and forces - Coulomb's law, Biot-Savart law, Coulomb and Lorentz force, but in relation to point charges, no approximations.


These two deal with the same E and B fields, all the same constants are there, all the relations, divergence, curl, flux or whatever is there. There is nothing in 1. that is not in 2, but there are things in 2. that are not in 1. Were approximations for charge densities and current potentials in Maxwell's equations derived from the point particle equations or was it the other way around?

Born2bwire

Sure, here are two simple problems for you to work out.

1. What are the total fields produced by an electron that is moving in a circle of constant radius R and at some constant speed v? We will let v vary as we see fit. This can easily be done by assuming a constant B field applied normally to the plane of oscillation.

2. What are the total fields at some point (X, 0, 0) as a function of time produced by an electron located at the origin that starts at rest from t=-\infty to t = -0 and starts oscillating along the z-axis. The oscillations can be modeled as a harmonic oscillator of magnitude A and angular frequency \omega.