rotation of a body about a point with decreasing radius

Multiverse

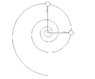
I have problem to see clearly the case of rotation of a body about a point with decreasing radius.this can be viewed as a body being rotated about a point with the help of a thread which passes through a hole in a disc and the thread is being pulled to apply a tension and gradually to decrease the length of the thread.I have attached a word doc. to have a clear pic. about it.It can seen that here that the instantaneous velocity has two components ,one perpendicular to the radius & other along radius. The tension is along the thread or radial.
there are some points to be noted.
1 .the tension being perpendicular cannot do any work on the perpendicular comp. of velocity & cannot change its magnitude.
2.there is no torque about the center as tension is radial. So, angular momentum should be conserved.
But the problem is angl. momen. is rXp . or " r*mv_{perpendicular}".
as angu. momen. is constant so r*mv_{perpendicular} should be constant.
Then if r decreases so then v_{perpendicular} must change. And it means that the perpendicular comp. of velocity changes ,which violate the 1st point.

Attached Files

Doc2.doc (26.0 KB, 12 views)

Doc Al

But as the thread is pulled, the velocity does develop a radial component and thus work is done. (The object spirals inward.) The speed of the object increases.

chrisbaird

Angular momentum is conserved and the perpendicular component of the velocity will increase. That is why figure skaters spin faster when they bring their arms in and why planets closer to their host star have faster orbits. Your error is in the first point.

rcgldr

Attached is an image that shows this situation. The short lines are perpendicular to the spiral path. It's also possible to reduce the force used to pull the string, in which case negative work is done, the object spirals outwards and the objects speed decreases:

Attached Thumbnails

 

Multiverse

thanks for your replies .All the statements made by you are absolutely right. Surely the speed of the revolving body will increase as the tension is doing work on it. The attachment given by "rcgldr" is OK. but have a look in this attachment below. the instantaneous velocity is (here in RED) tangential to the spiral path that the body makes. Now we resolve it into two comp.. one along the radius(in BLUE color) and the other perpendicular(in BLUE color) to it. ofcourse the ,the tension is acting along the radial direction and it doesnot have any comp. along the perpendicular component of the instantaneous velocity. So, the tension will do work on the radial velocity , as usually the net speed will increase .But .... the perpendicular component of the velocity will remain same. that is what I meant to say. The perpen. one will remain constant.

there is no torque about the center as tension is radial. So, angular momentum should be conserved.
But the problem is angl. momen. is rXp. or " r*mv_{perpendicular}".
as angu. momen. is constant so r*mv_{perpendicular} should be constant.
Then if r decreases so then v_{perpendicular} must change. And it means that the perpendicular comp. of velocity changes.

Attached Thumbnails

 

rcgldr

Only for an instant (zero time). As the object moves, the direction of the "perpendicular" component of velocity is constantly changing, so what was the radial component of velocity at one time becomes part of the perpendicular component at a later time.

It is constant. If the radius is decreased by 1/2 and then kept constant, then the speed of the object doubles and the tension increases by 8x. Some of the math (which shows work done equals change in kinetic energy) is included in post #3 of this thread:

http://www.physicsforums.com/showthread.php?t=328121

Multiverse

the direction will change , but magnitude should remain same as the tension cannot change the perpendicular component of the velocity because tension is always perpendicular to the per. comp. of velocity at any instant.

rcgldr

As I mentioned before since the direction is changing, then the radial component later ends up as part of the future perpendicular component. Take the case where the radius stops decreasing and becomes constant. If the new radius is 1/2 the original radius, then the objects speed is doubled, and all of that speed is perpendicular. Now take the case where the string is pulled inwards very slowly (assuming no losses here), where the spiral path is nearly circular. When the radius is 1/2 the original radius, the speed is doubled, and almost all of that speed is in the perpedicular component (because of the very slow radial movement).

chrisbaird

What exactly is the problem? You are right, no work is done in the tangential direction. That is why angular momentum is conserved and the speed must increase as the radius decreases. What part of this process is causing confusion.

Multiverse

may be you are right,but ,truly speaking I am not getting you. I am just a beginner. It will be my privillage if you can just ellaborate this concept and clear the errors in my thinking.You can suggest some links also .
I saw this link . "the involute of circle " ,this stuff really helped me to do one problem or two in Irodov. but even after solving them correctly ,I am confussed.

Sir, here the tangential velocity to the spiral path is the instanteneous velocity. It has two components -'one along radius and other perpendicular to it'. The perpendicular component of this instanteneous velocity is not the tangential velocity (which is in tangential direction to the spiral path).
So, tention , being perpendicular to this perpendicular component, can change its(perpendicular component's) direction but not the magnitude ofcourse.
So, clearly
1.Angular momentum is constant .
2.the V_{perpendicular} is constant in magnitude.
Now my confussion is:-
Since, Angular momentum is constant,its direction and magnitude both must remain constant.
The expression for angular momentum is rxV .

ignoring its direction which always remains same,it can be written simply as
........................magnitude of angular momentum = r.V_{perpendicular}.............
Since,its magnitude is also constant , if 'r' decreases then V_{perpendicular} must also change.
This is my confussion because V_{perpendicular} is constant (as you also agreed) .
This miraculas result is really disturbing me.

rcgldr

The string is causing the object's direction to change as well as the object's speed. The velocity tangental to the path of the object as the string is pulled inwards is increasing. The "perpendicular" component of that velocity will also increase over time. This is because as the direction of the velocity changes, so does the direction of the component considered to be "perpendicular".

For example, there's a moment in time when that direction of the perpendicular component of velocity is horizontal. Prior to that moment in time, there was a period of time when there was acceleration in the horizontal direction. Only at the instant of that moment in time is there no acceleration in the horizontal direction. Immediately afterwards, there will be a decleration in the horizontal direction because the direction is being changed towards vertical (assuming a spiral like path).

As long as the string is being pulled inwards or released outwards, the velocity and the components of that velocity will be continously changing.

Multiverse

OK, I got your point.Really it is quite satisfying.
But now take the similar case when a body is in just a simple circular motion. The instantaneous velocity and tangential velocity is same here.This velocity is always perpendicular to the tension. Now going with your same logic, suppose there was a moment in time when the string is vertical and the instantaneous velocity is horizontal. Before this ,there was a period of time, it had acceleration along horizontal direction because of tension . So,this component of tension should also change the magnitude this velocity .But as we know that the tangential velocity ,which is also always perpendicular to the radius, is constant in magnitude.

rcgldr

In the circular path case, using the moment in time when the tangental direction is horizontal, then prior to that, there was acceleration in the horizontal direction, but in this case it's all due to a change in direction from vertical to horizontal, because in the circular path case, there is no change in speed. The horizontal component of speed increases until the tangental component becomes horizontal, then it decreases as the horizontal component goes to zero and the tangental component transitions to vertical, and vice versa.

The main thing to consider is if there is any component of acceleration in the direction of (or opposing) velocity, then the magnitude of velocity, |V| will change. Unless the path is a straight line in the direction of the string, the string is rotating, and as I mentioned before since the direction is changing, then a radial component later ends up as part of the future perpendicular component.