EPFLstudent
- 2
- 0
Figure attached below. You have a big block of mass M and a small block of mass m. When m=3kg, the acceleration of the large block is 0.6ms-2. When m=4kg, the acceleration of the large block is 1.6ms-2. The dynamic friction coefficient between the large block and the surface it slides on is μ. There is no friction between any other surface. Questions:
a) Express the relationship between the movement of block m and block M
b) Derive expressions for the motion of block m and block M.
c) Determine the mass of block M and the dynamic friction coefficient, μ, between it and the surface it slides on.
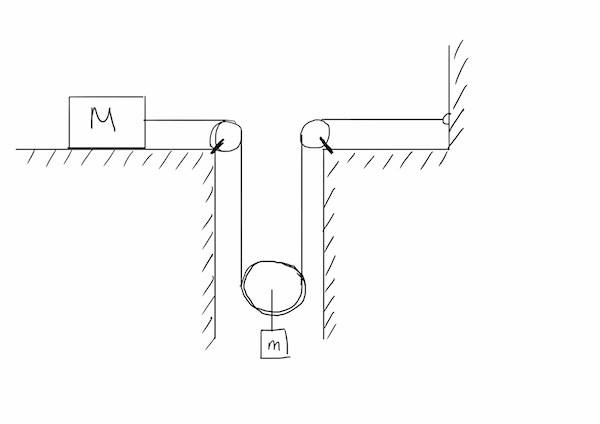
a) Express the relationship between the movement of block m and block M
b) Derive expressions for the motion of block m and block M.
c) Determine the mass of block M and the dynamic friction coefficient, μ, between it and the surface it slides on.
Last edited: