- #1
yungman
- 5,755
- 292
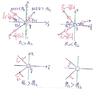
Attached are the drawings. Does the polarity Eof depend on [itex] \Gamma =\frac {\eta_2-\eta_1}{\eta_2+\eta_1}[/itex]
So if [itex]\eta_2<\eta_1[/itex], the Γ is negative and the polarity of the reflected wave is opposite polarity?
I understand [itex]\theta_i=\theta_r[/itex] and all that. As shown in the drawing, if you look at the TEM wave travel from the left at z=-ve, in medium 1, hitting the boundary on xy plane at z=0, say it is perpendicular polarization where [itex]\vec {E}= \hat {y} E(z)[/itex], which is parallel to the boundary. If [itex]\eta 1 > \eta 2\;\Rightarrow\; \Gamma=-ve[/itex], is [itex] \vec {E}_r[/itex] in opposite direction...[itex]\vec {E}_r=-\hat {y} E_r[/itex] as in the upper left drawing.
And if [itex]\eta 2 > \eta 1\;\Rightarrow\; \Gamma = +ve[/itex], then [itex] \vec {E}_r=\hat{y}E_r[/itex]. This is shown in the upper right drawing.
The upper left shows [itex]\eta 1 > \eta 2 [/itex] where Ei and Er are pointing in y direction. In drawing on top right where [itex]\eta 1 < \eta 2 [/itex], Er is in -ve y direction.
I drew the case where Ei is on the xz plane as shown in lower left drawing, how do I even determine the direction of the reflection based on the intrinsic impedance of the two media? Please help. Please provide some article links if you can.
Thanks
Alan
So if [itex]\eta_2<\eta_1[/itex], the Γ is negative and the polarity of the reflected wave is opposite polarity?
I understand [itex]\theta_i=\theta_r[/itex] and all that. As shown in the drawing, if you look at the TEM wave travel from the left at z=-ve, in medium 1, hitting the boundary on xy plane at z=0, say it is perpendicular polarization where [itex]\vec {E}= \hat {y} E(z)[/itex], which is parallel to the boundary. If [itex]\eta 1 > \eta 2\;\Rightarrow\; \Gamma=-ve[/itex], is [itex] \vec {E}_r[/itex] in opposite direction...[itex]\vec {E}_r=-\hat {y} E_r[/itex] as in the upper left drawing.
And if [itex]\eta 2 > \eta 1\;\Rightarrow\; \Gamma = +ve[/itex], then [itex] \vec {E}_r=\hat{y}E_r[/itex]. This is shown in the upper right drawing.
The upper left shows [itex]\eta 1 > \eta 2 [/itex] where Ei and Er are pointing in y direction. In drawing on top right where [itex]\eta 1 < \eta 2 [/itex], Er is in -ve y direction.
I drew the case where Ei is on the xz plane as shown in lower left drawing, how do I even determine the direction of the reflection based on the intrinsic impedance of the two media? Please help. Please provide some article links if you can.
Thanks
Alan
Attachments
Last edited: