quickclick330
- 82
- 0
Quick integrating question...(part of a series question)
Still studying for my exam...
Came across this example and I don't know what the method is for integrating this type of problem? (I'm using it to do the integral test for series). How did they get rid of the x^3? thanks for the help :-)
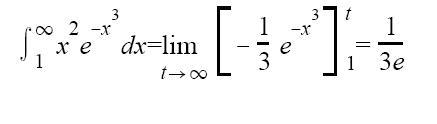
Still studying for my exam...
Came across this example and I don't know what the method is for integrating this type of problem? (I'm using it to do the integral test for series). How did they get rid of the x^3? thanks for the help :-)