vasra
- 5
- 0
Hello, new poster here.
I have trouble understanding some friction/resistance properties and how they are applied to rolling & linear motion simultaneously.
I've done a lot of simple static / dynamic (sliding) friction examples as well as rolling without taking into account resistance, but somehow the combination seems somewhat counter-intuitive to me.
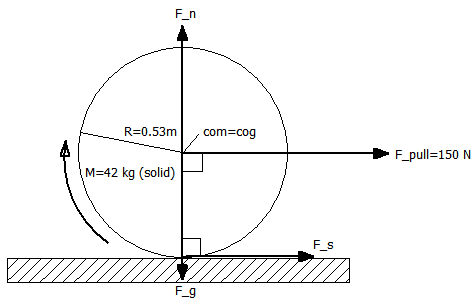
Solid cylinder on a horizontal surface is pulled from it's center of gravity (cog = com) parallel to the surface with force F_p=150N. See the free body diagram above. The known variables are:
R=0.53m (radius of the cylinder end)
M=42kg (mass of the solid cylinder)
F_p=150N (force pulling the com of cylinder)
\mu=0.3 (friction coefficient between cylinder and surface)
Define the (linear) acceleration of the cylinder and the angular acceleration of the cylinder, when the friction coefficient between the cylinder and surface is \mu=0.3
Personal notes
There is no specific information about:
- whether the cylinder rolls, slides or both
- friction is not identified other than being friction (assume static friction either at rest or static friction at rolling motion
- is the friction given a constant or maximum value for the friction (both static friction at rest and rolling resistance are variable : they are relative to the forces being applied)?
0. In a case like this, how do I identify (or do I _have_ to identify) what the given friction coefficient means? I assume it is for static friction, but can I infer it somehow?
1. In the image above (drawn by me, may be incorrect). The direction of the rolling resistance is in the same direction as the the force pulling the cylinder, trying to cause movement, right? (this is due to the fact that the rolling should be clockwise in this case and rolling resistance should resist that clockwise motion of cylinder's surface particles when touching the level surface, effectively preventing slipping up to a point).
Fix co-ordinate: Positive directions towards up and down.
Attempt 1.
\Sigma F=F_r=F_g-F_N+F_p-F_s
The sum of forces is (resultant force): Gravity and normal forces are equal, but opposite in direction, force that pulls is resisted by the static friction force.
F_g=Mg, F_s=\mu F_N=\mu Mg, F_r=Ma
F_r=Ma=F_p-\mu Mg \leftrightarrow a=(F_p-\mu Mg) \div M
This gives an answer in the correct units, but I have no intuitive way of checking whether the magnitude of the answer feels realistic.
Also, somehow I'm not sure, because:
1. A dynamic (sliding) friction would indeed resist the pulling force (in a simplified case) and turn the energy into heat, sound and possible deformation (?).
2. A static friction causes the cylinder to rotate, helping to convert linear motion to angular motion. IF the static friction is transferring part of the pulling linear force to the rotation of the cylinder, but also resisting the linear motion itself (as heat loss?), then how do I separate these? Do I have to?
3. I really can't put my finger down on this, but somehow the above feels unintuitive.
I've been looking at:
- Fundamentals of physics, 8th ed (Walker)
- Conceptual Physics, 10th ed (Hewitt)
- College Physics, 7th (Serwa7)
but all the explanations are really simplistic and I can't seem to be able to understand the concept of combined linear + rolling motion w/ friction applied and thus, cannot be sure if my above FBD and subsequent calculations are anywhere correct.
BTW, from above, if it's correct, I'd continue by applying the rotational inertia equation for a solid cylinder, noting that the the friction force works as torque, which in turn is equal to the inertia times angular acceleration and from there working the angular acceleration.
On a related note:
Once I'm done and I'm not sure if I've correctly understood the situation and it's dynamics, what other ways of checking the validity of my problem solving do I have, other than:
- calculate with and check for correct units (esp. the answer)
- compare if the result is within realistic ballpark figure (sometimes really difficult, unless I'm in a lab or have access to measurement data)
I have trouble understanding some friction/resistance properties and how they are applied to rolling & linear motion simultaneously.
I've done a lot of simple static / dynamic (sliding) friction examples as well as rolling without taking into account resistance, but somehow the combination seems somewhat counter-intuitive to me.
Homework Statement
Solid cylinder on a horizontal surface is pulled from it's center of gravity (cog = com) parallel to the surface with force F_p=150N. See the free body diagram above. The known variables are:
R=0.53m (radius of the cylinder end)
M=42kg (mass of the solid cylinder)
F_p=150N (force pulling the com of cylinder)
\mu=0.3 (friction coefficient between cylinder and surface)
Define the (linear) acceleration of the cylinder and the angular acceleration of the cylinder, when the friction coefficient between the cylinder and surface is \mu=0.3
Personal notes
There is no specific information about:
- whether the cylinder rolls, slides or both
- friction is not identified other than being friction (assume static friction either at rest or static friction at rolling motion
- is the friction given a constant or maximum value for the friction (both static friction at rest and rolling resistance are variable : they are relative to the forces being applied)?
Homework Equations
0. In a case like this, how do I identify (or do I _have_ to identify) what the given friction coefficient means? I assume it is for static friction, but can I infer it somehow?
1. In the image above (drawn by me, may be incorrect). The direction of the rolling resistance is in the same direction as the the force pulling the cylinder, trying to cause movement, right? (this is due to the fact that the rolling should be clockwise in this case and rolling resistance should resist that clockwise motion of cylinder's surface particles when touching the level surface, effectively preventing slipping up to a point).
The Attempt at a Solution
Fix co-ordinate: Positive directions towards up and down.
Attempt 1.
\Sigma F=F_r=F_g-F_N+F_p-F_s
The sum of forces is (resultant force): Gravity and normal forces are equal, but opposite in direction, force that pulls is resisted by the static friction force.
F_g=Mg, F_s=\mu F_N=\mu Mg, F_r=Ma
F_r=Ma=F_p-\mu Mg \leftrightarrow a=(F_p-\mu Mg) \div M
This gives an answer in the correct units, but I have no intuitive way of checking whether the magnitude of the answer feels realistic.
Also, somehow I'm not sure, because:
1. A dynamic (sliding) friction would indeed resist the pulling force (in a simplified case) and turn the energy into heat, sound and possible deformation (?).
2. A static friction causes the cylinder to rotate, helping to convert linear motion to angular motion. IF the static friction is transferring part of the pulling linear force to the rotation of the cylinder, but also resisting the linear motion itself (as heat loss?), then how do I separate these? Do I have to?
3. I really can't put my finger down on this, but somehow the above feels unintuitive.
I've been looking at:
- Fundamentals of physics, 8th ed (Walker)
- Conceptual Physics, 10th ed (Hewitt)
- College Physics, 7th (Serwa7)
but all the explanations are really simplistic and I can't seem to be able to understand the concept of combined linear + rolling motion w/ friction applied and thus, cannot be sure if my above FBD and subsequent calculations are anywhere correct.
BTW, from above, if it's correct, I'd continue by applying the rotational inertia equation for a solid cylinder, noting that the the friction force works as torque, which in turn is equal to the inertia times angular acceleration and from there working the angular acceleration.
On a related note:
Once I'm done and I'm not sure if I've correctly understood the situation and it's dynamics, what other ways of checking the validity of my problem solving do I have, other than:
- calculate with and check for correct units (esp. the answer)
- compare if the result is within realistic ballpark figure (sometimes really difficult, unless I'm in a lab or have access to measurement data)
Last edited: