- #1
Cleonis
Gold Member
- 732
- 39
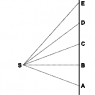
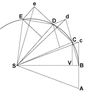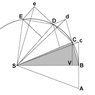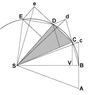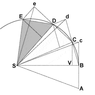
In the image above the line ABCDE represents the trajectory of a point mass, in inertial motion. Point S is in inertial motion also. As we know, in inertial motion equal distances are covered in equal intervals of time.
All of the consecutive triangles (SAB, SBC, etc) have the same area, as they have the same base and same height. This implies that equal areas are swept out in equal intervals of time.
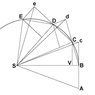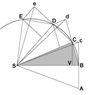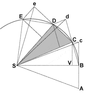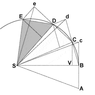
The image below reproduces Newton's demonstration that Kepler's law of areas follows from the laws of motion.
A point mass is traveling along the curvilinear trajectory BCDE
Point S represents the common center of mass of two point masses that attract each other. It follows from the third law that point S is in inertial motion. The force upon the traveling point mass is at all times towards point S.
Without any force the point mass would proceed to point c. At point B the point mass receives an impulse towards S. The resulting motion is the vector sum of the original velocity and the added velocity component. This algorithm is repeated over the length of the curve.
The consecutive triangles all have the same area. In the limit of infinitisimal time increments the segments produce the curve.
I think these geometric demonstrations illustrate that angular momentum is a compound entity, reducible to elements. The elements of angular momentum are Newton's laws of motion.