You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
AI Thread Summary
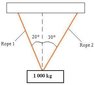
To determine if either rope supporting a 1000 kg steel beam will break under a maximum tension of 6000N, the forces acting on the system must be analyzed. The total weight of the beam is approximately 10000N, which must be balanced by the vertical components of the tensions in the ropes. The equations derived from the free body diagram are F1 sin[20] + F2 sin[30] = 10000 for vertical forces and F1 cos[20] - F2 cos[30] = 0 for horizontal forces. By solving these equations, the tensions F1 and F2 can be calculated to see if they exceed the maximum tension limit of 6000N. This analysis will confirm whether either rope will break under the given load conditions.
Physics news on Phys.org
Galileo
Science Advisor
Homework Helper
- 1,980
- 7
Draw a free body diagram.
The two tensions are directed along the ropes.
The sum of the tensions is directed upwards and has magnitude F=mg (m=mass of the beam).
The two tensions are directed along the ropes.
The sum of the tensions is directed upwards and has magnitude F=mg (m=mass of the beam).
xepma
- 525
- 8
Well, the weight causes a force of roughly 10*1000 = 10000 [N] on both ropes combined. But because of different angles, the forces caused by the ropes will not be the same. Let F1 be the force of the left rope (20 degree angle), and F2 the other force.
You know that the forces will have to keep the weight up, so the vertical components together must add up to 10000 [N] :
F1 sin[20] + F2 sin[30] = 10000
Now the horizontal components will be directed in opposite direction, and will, because of that, have to be of equal size. So:
F1 cos[20] - F2 cos[30] = 0
You can solve F1 and F2 from these equations, and check if any of the ropes will break.
You know that the forces will have to keep the weight up, so the vertical components together must add up to 10000 [N] :
F1 sin[20] + F2 sin[30] = 10000
Now the horizontal components will be directed in opposite direction, and will, because of that, have to be of equal size. So:
F1 cos[20] - F2 cos[30] = 0
You can solve F1 and F2 from these equations, and check if any of the ropes will break.
Last edited:
Kindly see the attached pdf. My attempt to solve it, is in it.
I'm wondering if my solution is right. My idea is this: At any point of time, the ball may be assumed to be at an incline which is at an angle of θ(kindly see both the pics in the pdf file). The value of θ will continuously change and so will the value of friction.
I'm not able to figure out, why my solution is wrong, if it is wrong .
TL;DR Summary: I came across this question from a Sri Lankan A-level textbook.
Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water.
I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...
I can't figure out how to find the velocity of the particle at 37 degrees. Basically the bead moves with velocity towards right let's call it v1. The particle moves with some velocity v2. In frame of the bead, the particle is performing circular motion. So v of particle wrt bead would be perpendicular to the string. But how would I find the velocity of particle in ground frame?
I tried using vectors to figure it out and the angle is coming out to be extremely long. One equation is by work...
Similar threads
- Replies
- 2
- Views
- 1K
- Replies
- 8
- Views
- 10K
- Replies
- 43
- Views
- 4K
- Replies
- 1
- Views
- 3K
- Replies
- 22
- Views
- 8K
- Replies
- 22
- Views
- 417
- Replies
- 23
- Views
- 7K
- Replies
- 5
- Views
- 2K
- Replies
- 1
- Views
- 1K
- Replies
- 7
- Views
- 4K
Hot Threads
-
Work Done in slowly pulling a thread
- Started by Bling Fizikst
- Replies: 28
- Introductory Physics Homework Help
Recent Insights
-
Insights Thinking Outside The Box Versus Knowing What’s In The Box
- Started by Greg Bernhardt
- Replies: 1
- Other Physics Topics
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 28
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math