Lolsauce
- 21
- 0
So I'm currently reviewing for my electromagnetism class, but I do not remember the techniques from going to phasor to instantaneous time. Maybe someone can explain to me what is going on.
Find the instantaneous time sinusoidal functions corresponding to the following phasors:My question is specifically on Part A and Part B
Relevant equations includes Eulers:
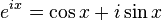
Which let you go from polar to rectangular.
For Part A, we are given V~ = -5exp(j*pi/3)
I just went straight from phasor to instantaneous time:
V~ = v(t) -> -5exp(j*pi/3) = Re{V~ * exp(jwt) = -5exp(jwt + pi/3)
But for some strange reason, in the solution manual they subtract pi from the exponential to remove the negative sign. I'm not exactly sure why they do this. It is the same for Part B, why do they subtract pi/2. Can anyone explain this to me? I've also attached the solution to part A and B below.
Homework Statement
Find the instantaneous time sinusoidal functions corresponding to the following phasors:My question is specifically on Part A and Part B
Homework Equations
Relevant equations includes Eulers:
Which let you go from polar to rectangular.
The Attempt at a Solution
For Part A, we are given V~ = -5exp(j*pi/3)
I just went straight from phasor to instantaneous time:
V~ = v(t) -> -5exp(j*pi/3) = Re{V~ * exp(jwt) = -5exp(jwt + pi/3)
But for some strange reason, in the solution manual they subtract pi from the exponential to remove the negative sign. I'm not exactly sure why they do this. It is the same for Part B, why do they subtract pi/2. Can anyone explain this to me? I've also attached the solution to part A and B below.
Last edited by a moderator: