Electric Field of extended mass

Redoctober

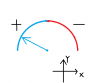
So here is the scenario (see attachment) - I have a semicircle wire (radius R=15.9cm) which is made of insulator material , the semicircle consist of two combined quartercircle wires parts where one has equally distributed charge +Q and the other has -Q . Required is find the Electric field in direction of x at the origin . Q=5.33nC

My approach was as follows

Let E = 1/(4*pi*e)∫1/(R^2).dQ r

dQ=λ*ds and ds=R*dθ and i also know that unit vector r = cosθ*i+sinθ*j

therefore for the E in x direction i get this expression

E = 1/(4*pi*e)*1/(R^2)*λ*R∫cosθ.dθ

Integrating from 0 to pi ( thus taking only half of the semicircle ) and using λ as 2/(pi*r)

I get Q/(2*pi^2*e*R^2) .
Because the other half has opposite charge i can say that the Etot = Eneg +Epos

Therefore i multiply the equation by two to finaly get

Q/(pi^2*e*R^2)

If i put the values given i get as absolute value 2413 N/C for Electric field at origin of circel in the direction of x

Unfortunately it is a wrong solution :( !! What is the mistake i hv done ?? Can anyone spot it ? Thanks in advance

Attached Thumbnails

 

tiny-tim

Hi Redoctober!
noooo …

0 to π/2

Redoctober

Oh !! srrry typo error :S :S , i integrated from 0 to pi/2 .
The answer 2413 N/C is wrong :/ !

Redoctober

Anyone has a solution ?? :/ !

JHamm

The E field for the right part of your semi circle is given by
[tex]E = \int_0^{\frac{\pi}{2}} \frac{-Q}{4\pi\epsilon_0r^2} d\theta[/tex]
While the E field for the left part is the same but with +Q charge and integrated from [itex]\frac{\pi}{2}[/itex] to [itex]\pi[/itex]. Just add these two together to get the total field.

vanhees71

Are you sure? An electric field is a vector, and the correct formula is

[tex]\vec{E}(\vec{x})=\frac{1}{4 \pi \epsilon_0} \int_{\mathbb{R}^3} \rho(\vec{x}') \frac{\vec{x}-\vec{x}'}{|\vec{x}-\vec{x}'|^3}.[/tex]

Of course, in the here considered case, you have to integrate along the semicircle and use the charge per length instead of the bulk-charge density. However, you should check, whether you have all the geometrical factors for you vector component right.

Redoctober

Vanhees is right , Electric field is a vector .
So regarding the E will be in radial direction .
For the Y axis we need to consider the j component .

Vanhees , your mathematical expression is a bit high beyond my math skill xD !

My question is why the final expression for the problem is wrong :/

i considered the +Q and -Q E vector addition

I reached to the conclusion of

|E| = Q/(4*pi^2*e*r^2) (In the direction of J

Btw : how do u write the math expressions in that style xD . my way of typing the math is silly :/ !!

Redoctober

The final equation i got was actually correct

i made an error with the calculation thats why my answer was wrong :)

vanhees71

Yes, I've checked your result too. It's correct. I parametrized the line charge with help of the charge per angle:

[tex]\lambda(\varphi)=\begin{cases}
-\frac{2 Q}{\pi} & \text{for} \quad 0 \leq \varphi \leq \pi/2 \\
+\frac{2Q}{\pi} & \text{for} \quad \pi/2<\varphi\leq \pi \\
0 & \text{elsewhere}.
\end{cases}
[/tex]

Then you can use my formula for [itex]\vec{x}=0[/itex] to get

[tex]\vec{E}=\frac{1}{4 \pi \epsilon_0 r^2} \int_0^{2 \pi} \mathrm{d} \varphi' \lambda(\varphi') \begin{pmatrix} -\cos \varphi' \\ -\sin \varphi' \\0 \end{pmatrix}.[/tex]

Integrating over the two regions gives finally

[tex]\vec{E}=\frac{Q}{\pi^2 \epsilon_0 r^2} \vec{e}_x.[/tex]