Homework Help Overview
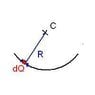
The discussion revolves around understanding the electric potential (V) of an arc of uniform charge, particularly why it can be treated similarly to a point charge. The subject area includes concepts of electric potential, charge distribution, and the comparison between different geometries in electrostatics.
Discussion Character
- Conceptual clarification, Assumption checking
Approaches and Questions Raised
- The original poster attempts to understand the reasoning behind treating an arc as a point charge, questioning if this relates to the properties of a conducting sphere. Other participants discuss the nature of electric potential as a scalar quantity and how contributions from different charge elements can be summed to find the total potential.
Discussion Status
Participants are exploring the relationship between electric potential and charge distribution, with some providing insights into the mathematical treatment of the problem. There is an acknowledgment of the confusion surrounding related concepts such as electric force and electric field, indicating an ongoing exploration of these ideas.
Contextual Notes
Some participants express confusion regarding the distinctions between electric force, electric field, electric potential, and electric potential energy, which may affect their understanding of the problem at hand.