- #1
karush
Gold Member
MHB
- 3,269
- 5
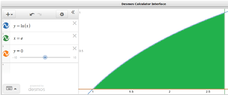
Find the mass and centroid of the following thin plate assuming constant density
Sketch the region corresponding
to the plate and indicate the location
of the center is the mass
The region bounded by
$$y=ln x$$
$$x-axis$$
$$x=e$$
\begin{align}\displaystyle
\left(\overline{x},\overline{y}\right)
&=\left(\frac{my}{m}\frac{mx}{m}\right)\\
m&=\int_{a}^{b}\int_{a}^{b}xy \, dA\\
&=\int_{1}^{e}\int_{0}^{\ln{x}}xy \, dydx\\
&=\int_{1}^{e}x\left[\int_{1}^{\ln{x}} y \, dy\right]dx\\
&=\int_{1}^{e}x\left[ \frac{y^2}{2}\right]_0^{\ln{x}} \ dx\\
&=\int_{1}^{e}x\ln{x} \, dx\\
W|A &=\frac{1}{4}\left(1+e^2 \right)
\end{align}
so ?
the centroid is:
$$\left[\frac{e^2+1}{4},\frac{e}{2}-1\right]$$
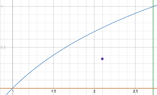
Sketch the region corresponding
to the plate and indicate the location
of the center is the mass
The region bounded by
$$y=ln x$$
$$x-axis$$
$$x=e$$
\begin{align}\displaystyle
\left(\overline{x},\overline{y}\right)
&=\left(\frac{my}{m}\frac{mx}{m}\right)\\
m&=\int_{a}^{b}\int_{a}^{b}xy \, dA\\
&=\int_{1}^{e}\int_{0}^{\ln{x}}xy \, dydx\\
&=\int_{1}^{e}x\left[\int_{1}^{\ln{x}} y \, dy\right]dx\\
&=\int_{1}^{e}x\left[ \frac{y^2}{2}\right]_0^{\ln{x}} \ dx\\
&=\int_{1}^{e}x\ln{x} \, dx\\
W|A &=\frac{1}{4}\left(1+e^2 \right)
\end{align}
so ?
the centroid is:
$$\left[\frac{e^2+1}{4},\frac{e}{2}-1\right]$$
Last edited: