jlewallen18
- 6
- 0
Homework Statement
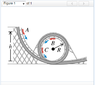
A car in an amusement park ride rolls without friction around the track shown in the figure (Figure 1) . It starts from rest at point A at a height h above the bottom of the loop. Treat the car as a particle.
If the car starts at height h= 5.00 R and the radius is R = 16.0m , compute the speed of the passengers when the car is at point C, which is at the end of a horizontal diameter.
Homework Equations
Conservation of Energy
The Attempt at a Solution
Using conservation of Energy
PE_i + KE_i = PE_f + KE_f
mgh = mgh + 1/2mv^2
mg(5R) = mg(R) + 1/2mv^2 (We are solving for V, so..)
mg(5R) - mg(R) = 1/2mv^2
(Cancel out mass)
g(5R) - g(R) = 1/2v^2
2(g(5R) - g(R)) = v^2
sqrt(2(g(5R) - g(R))) = V
(Plug in R)
sqrt(2(g(80) - g(5))) = V
If this is correct so far, is g just gravity or is it centripetal acceleration? I loose confidence at this step..Lead me in the right direction?
Thanks!