- #1
whit3r0se-
- 20
- 2
Ever since the discovery of Pi, Mathematicians have been obsessed with finding methods of approximating Pi. I think I've a unique way of doing so via the Newton-Raphson.
Newton-Raphson Formula:
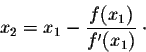
Let ## ƒ(x)=Sin(x) ⇒ ƒ'(x)=Cos(x) ⇒ X_n= X_{n-1} - tan(X_{n-1})##
For example: Let ##X_0=X ⇒ X_3= (X-tan(X)-tan(X-tan(X))) - tan(X-tan(X)-tan(x-tan(X)))##
This cannot be calculated without a calculator therefore we can introduce a taylor expansion:
##Tan(x)≈x+x^3/3+(2 x^5)/15+(17 x^7)/315+...##
NOTE: For this to work the value of ##X_0 ## must be close to Pi, the rate of convergence is proportional to how close your value of ##X_0## is to Pi.
I'd appreciate any feedback on this method and ways to simplify/generalise my equation.
Newton-Raphson Formula:
Let ## ƒ(x)=Sin(x) ⇒ ƒ'(x)=Cos(x) ⇒ X_n= X_{n-1} - tan(X_{n-1})##
For example: Let ##X_0=X ⇒ X_3= (X-tan(X)-tan(X-tan(X))) - tan(X-tan(X)-tan(x-tan(X)))##
This cannot be calculated without a calculator therefore we can introduce a taylor expansion:
##Tan(x)≈x+x^3/3+(2 x^5)/15+(17 x^7)/315+...##
NOTE: For this to work the value of ##X_0 ## must be close to Pi, the rate of convergence is proportional to how close your value of ##X_0## is to Pi.
I'd appreciate any feedback on this method and ways to simplify/generalise my equation.
Last edited by a moderator: