Archimedes' area of a sphere proof; proposition 2

[Ebenshap]

Hi,

I wanted to see if I could understand Archimedes' proof for the area of a sphere directly from one of his texts. Almost right away I was confused by the language. Archimedes lists a bunch of propositions that eventually lead up to the 25th proposition where the area of the sphere is finally explained. But I'm stuck on the 2nd proposition. I can accept that this proof is true, but I don't get why it's noteworthy.

Here's the text for the proposition:

Given two unequal magnitudes, it is possible to find two unequal straight lines such that the greater straight line has to the less a ratio less than the greater magnitude has to the less.

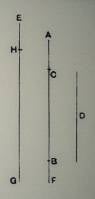
Let AB, D represent the two unequal magnitudes, AB being the greater.

Suppose BC measured along BA equal to D, and let GH be any straight line.

Then, if CA be added to itself a sufficient number of times, the sum will exceed D. Let AF be this sum, and take E on GH produced such that GH is the same multiple of HE that AF is of AC.

Thus EH/GH=AC/AF

But, since AF > D (or CB), then AC/AF<AC/CB

Therefore, componendo,

EG/GH < AB/D

Hence EG, GH are two lines satisfying the given condition.
​

I looked up componendo and it means to transform a fraction by adding it's denominator to it's numerator, so that this:
EH/GH
becomes this:
(EH +GH)/GH which is equal to EG/GH

Why does Archimedes think this is important to establish to figure out the area of a sphere? And also what's the difference in this example between a magnitude and a line. From the language used here, they seem to be the same thing but there must be a difference. Maybe a magnitude is a line and a line is a line segment?

Thank you,

Eben

 

[pbuk]

Firstly you are not studying "directly from one of his texts". You are studying a compilation of translations of copies of copies of translations, and while a great deal of study has gone into the modern texts this process is not perfect.

Secondly you must remember that Archimedes did not have the tools of modern mathematics available to him, so he has to prove a lot of things that we take for granted. This also means that most of Archimedes' proofs are not based on the axioms on which modern mathematics is based so are only of historical interest.

To answer your question "why does Archimedes think this is important" you only have to read on in the text - Prop. 2 is used in the second stage of Prop. 3.

 

[Ebenshap]

Firstly you are not studying "directly from one of his texts". You are studying a compilation of translations of copies of copies of translations, and while a great deal of study has gone into the modern texts this process is not perfect.

Secondly you must remember that Archimedes did not have the tools of modern mathematics available to him, so he has to prove a lot of things that we take for granted. This also means that most of Archimedes' proofs are not based on the axioms on which modern mathematics is based so are only of historical interest.

To answer your question "why does Archimedes think this is important" you only have to read on in the text - Prop. 2 is used in the second stage of Prop. 3.

Thanks MrAnchovy,

You're right, my interest in this is historical. I suppose I meant to say that I would like to study the earliest recording that I could easily get on my kindle. At first it seemed to me the proof was to show that unequal ratios exist. And that to me seems unnecessary to prove. After a closer reading I think he's saying that it's possible to derive a pair of unequal lines from another pair of unequal lines, and more specifically that it's possible to do that derivation in a way where the ratio of the derived pair of unequal lines is less than the ratio of the original pair of unequal lines. The key word in there was 'to find.'

It's interesting how abstract the language is to include as wide a range of different line pairs as possible. That's pretty sophisticated, especially for being over 2000 years old.