Exploring Arc Lengths and Curves

[mathmari]

Hey!

In some notes that I am reading there is the following:

View attachment 4793

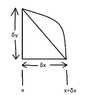
$$(\delta s)^2=(\delta x)^2+(\delta y)^2 \Rightarrow \left (\frac{\delta s}{\delta x}\right )^2=1+\left (\frac{\delta y}{\delta x}\right )^2$$ When $\delta x \rightarrow 0 $ we get $$(s'(x))^2=1+(y'(x))^2 \Rightarrow s'(x)=\sqrt{1+(f'(x))^2} \Rightarrow s(x)=\int_A^x \sqrt{1+(f'(s))^2}ds$$



I have understood it as follows:

We have the curve $s$ and $\delta s$ is an approximation of the curve, so we get the triangle $\delta x$, $\delta y$, $\delta s$ and we apply the Pythagorean Theorem to get $(\delta s)^2=(\delta x)^2+(\delta y)^2$. This is equal to $\left (\frac{\delta s}{\delta x}\right )^2=1+\left (\frac{\delta y}{\delta x}\right )^2$.

From the limit $$s'(x)=\lim_{h \rightarrow 0}\frac{s(x+h)-s(x)}{h}=\lim_{h \rightarrow 0}\frac{\delta s}{h}$$ (resp. $y'(x)$) for $h=\delta x$ we get $(s'(x))^2=1+(y'(x))^2$.

Then taking the square root of the last equality we get $s'(x)=\pm \sqrt{1+(y'(x))^2}$.

Why do we take only the positive one, $s'(x)=\sqrt{1+(y'(x))^2}$ ?

After that we take integral to get $s(x)$.

Is everything correct?

Is $s(x)$ the curve or the arc length ?


After that there is the following:

$\sigma : [0, 1] \rightarrow \mathbb{R}^2 \text{ or } \mathbb{R}^3$
$$I(\sigma )=\int_0^1 ||\sigma '(t)||dt$$
$$d\sigma (t)=\sigma '(t)dt \\ |ds|=||\sigma '(t)||dt \\\ \sigma (t)=(\sigma_1 (t), \sigma_2 (t), \sigma_3 (t)), t \in [0, 1] \\ ||\sigma '(t)||=\sqrt{(\sigma_1' (t))^2, (\sigma_2' (t))^2,( \sigma_3' (t))^2}$$

So when we have a function in $\mathbb{R}$ we use the formula $s(x)$ and when we have a function in $\mathbb{R}^2$ or $\mathbb{R}^3$ we use the last formula $I(\sigma )$ to calculate the arc length?

 

[I like Serena]

Why do we take only the positive one, $s'(x)=\sqrt{1+(y'(x))^2}$ ?

After that we take integral to get $s(x)$.

Is everything correct?

Is $s(x)$ the curve or the arc length ?

Hi mathmari! (Mmm)

The symbol $s$ represents the arc length.
A length is always positive, therefore we only look at the positive root.
$s(x)$ is the arc length of the curve from some starting point $A$ up to a point with coordinate $x$.
This only works if $x$ is monotonous while traversing the curve.

We have to be careful though.
There is a chance the $s$ is also used to represent the curve, which would be bad practice.
Properly it should be $\mathbf s$ that represents the curve, using a bold face to indicate that it's a vector instead of a scalar. (Nerd)

After that there is the following:

$\sigma : [0, 1] \rightarrow \mathbb{R}^2 \text{ or } \mathbb{R}^3$
$$I(\sigma )=\int_0^1 ||\sigma '(t)||dt$$
$$d\sigma (t)=\sigma '(t)dt \\ |ds|=||\sigma '(t)||dt \\\ \sigma (t)=(\sigma_1 (t), \sigma_2 (t), \sigma_3 (t)), t \in [0, 1] \\ ||\sigma '(t)||=\sqrt{(\sigma_1' (t))^2, (\sigma_2' (t))^2,( \sigma_3' (t))^2}$$

So when we have a function in $\mathbb{R}$ we use the formula $s(x)$ and when we have a function in $\mathbb{R}^2$ or $\mathbb{R}^3$ we use the last formula $I(\sigma )$ to calculate the arc length?

This is a more general representation that doesn't rely on whether the x coordinate is monotonous or not.
The symbol $\sigma$ has been chosen to represent the same thing as $s$, the arc length, just with a different parameter.
They are related as follows:
$$\sigma(t) = s(x(t))$$
where
$$x(t) = \sigma_1(t)$$
(Wink)

 

[mathmari]

$$(\delta s)^2=(\delta x)^2+(\delta y)^2 \Rightarrow \left (\frac{\delta s}{\delta x}\right )^2=1+\left (\frac{\delta y}{\delta x}\right )^2$$ When $\delta x \rightarrow 0 $ we get $$(s'(x))^2=1+(y'(x))^2 \Rightarrow s'(x)=\sqrt{1+(f'(x))^2} \Rightarrow s(x)=\int_A^x \sqrt{1+(f'(s))^2}ds$$

The symbol $s$ represents the arc length.
A length is always positive, therefore we only look at the positive root.
$s(x)$ is the arc length of the curve from some starting point $A$ up to a point with coordinate $x$.
This only works if $x$ is monotonous while traversing the curve.

We have to be careful though.
There is a chance the $s$ is also used to represent the curve, which would be bad practice.
Properly it should be $\mathbf s$ that represents the curve, using a bold face to indicate that it's a vector instead of a scalar. (Nerd)

At the point where we apply the Pythagorean theorem, does $s$ represent the curve or the arc length? And wht $\delta s$ ?

This is a more general representation that doesn't rely on whether the x coordinate is monotonous or not.
The symbol $\sigma$ has been chosen to represent the same thing as $s$, the arc length, just with a different parameter.
They are related as follows:
$$\sigma(t) = s(x(t))$$
where
$$x(t) = \sigma_1(t)$$
(Wink)

I see... (Sun)

 

[I like Serena]

At the point where we apply the Pythagorean theorem, does $s$ represent the curve or the arc length? And wht $\delta s$ ?

Let's just say that $\delta s$ represents a small distance along the curve, small enough to be considered straight so we can apply the Pythagorean theorem.
Adding up all $\delta s$ values will give us the curve length (in the limit). (Mmm)